点P是双曲线x2a2-y2b2=1(a>0，b>0)的右支上一点，其左，右焦点分别为F1，F2，直线PF1与以原点O为圆心，a为半径的圆相切于A点，线段PF1的垂直平分线恰好过点F2，则离心率的值为（）A.32

Question

点P是双曲线

(x2)/(a2)-(y2)/(b2)=1(a>0，b>0)的右支上一点，其左，右焦点分别为F₁，F₂，直线PF₁与以原点O为圆心，a为半径的圆相切于A点，线段PF₁的垂直平分线恰好过点F₂，则离心率的值为（　　）

A.

(3)/(2)

B.

(4)/(3)

C.

(5)/(3)

D.

(5)/(4)

Answer 1

由线段PF₁的垂直平分线恰好过点F₂，
可得|PF₂|=|F₁F₂|=2c，
由直线PF₁与以坐标原点O为圆心、a为半径的圆相切于点A，
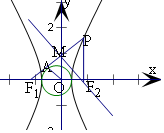
可得|OA|=a，
设PF₁的中点为M，由中位线定理可得|MF₂|=2a，
在直角三角形PMF₂中，可得|PM|=√(4c2-4a2)=2b，
即有|PF₁|=4b，
由双曲线的定义可得|PF₁|-|PF₂|=2a，
即4b-2c=2a，即2b=a+c，
即有4b²=（a+c）²，
即4（c²-a²）=（a+c）²，
可得a=(3)/(5)c，
所以e=(c)/(a)=(5)/(3)．
故选：C．