早教吧作业答案频道 -->数学-->
如图,已知抛物线y=ax2-5ax+2(a≠0)与y轴交于点C,与x轴交于点A(1,0)和点B.(1)求抛物线的解析式;(2)求直线BC的解析式;(3)若点N是抛物线上的动点,且点N在第四象限内,过点N
题目详情
如图,已知抛物线y=ax2-5ax+2(a≠0)与y轴交于点C,与x轴交于点A(1,0)和点B.
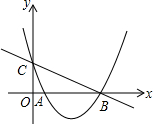
(1)求抛物线的解析式;
(2)求直线BC的解析式;
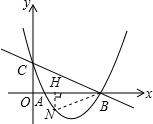
(3)若点N是抛物线上的动点,且点N在第四象限内,过点N作NH⊥x轴,垂足为H,以B,N,H为顶点的三角形是否能够与△OBC相似?若能,请求出所有符合条件点N的坐标;若不能,请说明理由.

(1)求抛物线的解析式;
(2)求直线BC的解析式;
(3)若点N是抛物线上的动点,且点N在第四象限内,过点N作NH⊥x轴,垂足为H,以B,N,H为顶点的三角形是否能够与△OBC相似?若能,请求出所有符合条件点N的坐标;若不能,请说明理由.
▼优质解答
答案和解析
 (1)∵点A(1,0)在抛物线y=ax2-5ax+2上,
(1)∵点A(1,0)在抛物线y=ax2-5ax+2上,
∴a-5a+2=0,∴a=
,
∴抛物线的解析式为:y=
x2-5ax+2;
(2)把x=0代入y=
x2-5ax+2,
解得:y=2,
∴C(0,2),
∵抛物线的对称轴为直线x=
,
∴B(4,0),
设直线BC的解析式为:y=kx+b,
∴
,
解得:k=-
,b=2,
∴直线BC的解析式为:y=-
x+2;
(3)设N(x,
x2-
x+2),
当△OBC∽△HBN时,如图,
∴
=
,
即
=
,
解得:x1=2,x2=4(不合题意舍去),
∴N(2,-1).
 (1)∵点A(1,0)在抛物线y=ax2-5ax+2上,
(1)∵点A(1,0)在抛物线y=ax2-5ax+2上,∴a-5a+2=0,∴a=
| 1 |
| 2 |
∴抛物线的解析式为:y=
| 1 |
| 2 |
(2)把x=0代入y=
| 1 |
| 2 |
解得:y=2,
∴C(0,2),
∵抛物线的对称轴为直线x=
| 5 |
| 2 |
∴B(4,0),
设直线BC的解析式为:y=kx+b,
∴
|
解得:k=-
| 1 |
| 2 |
∴直线BC的解析式为:y=-
| 1 |
| 2 |
(3)设N(x,
| 1 |
| 2 |
| 5 |
| 2 |
当△OBC∽△HBN时,如图,
∴
| OB |
| BH |
| OC |
| HN |
即
| 4 |
| 4-x |
| 2 | ||||
-(
|
解得:x1=2,x2=4(不合题意舍去),
∴N(2,-1).
看了 如图,已知抛物线y=ax2-...的网友还看了以下:
已知点A、B的坐标分别是(0,-1)、(0,1),|AB|是|MA|和|MB|的等差中项(1)求动点 2020-03-30 …
已知动点P的轨迹到定点A(2,0)的距离和它到定直线x=2分之1的距离比为2⑴求动点P的轨迹方程⑵若 2020-03-30 …
如图,点C是⊙O优弧ACB上的中点,弦AB=6cm,E为OC上任意一点,动点F从点A出发,以每秒1 2020-05-13 …
求轨迹数学题设动直线L垂直于X轴,且与椭圆x的平方加上二倍y的平方等于4交于A、B两点,P是L上满 2020-05-17 …
正方形ABCD的边长为6㎝,点E在AB上,AE=2㎝.动点F由点C开始以3㎝/s的速度沿折线CBE 2020-05-17 …
判断题:利用速度合成定理分析动点的运动时,动点的牵连速度是指某瞬时动系上与动点重合点的速度.() 2020-07-02 …
已知定点F(1,0),动点P在y轴上运动,过点P作PM交x轴于点M,并延长MP到点N,且,。(1) 2020-07-31 …
已知平面内点M(-3,2),N(5,-4),l是经过点A(-1,-2)且与MN垂直的直线,动点P( 2020-07-31 …
如图,三角形ABC为等边三角形,AB=6,P是AB上的一个动点知△ABC为等边三角形,AB=6,P 2020-08-03 …
(1)正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN,求证:MN平行 2021-02-16 …