早教吧作业答案频道 -->数学-->
在平面直角坐标系中,抛物线y=12x2经过点A(x1,y1)、C(x2,y2),其中x1、x2是方程x2-2x-8的两根,且x1<x2,过点A的直线l与抛物线只有一个公共点(1)求A、C两点的坐标;(2)求直线l的解
题目详情
在平面直角坐标系中,抛物线y=
x2经过点A(x1,y1)、C(x2,y2),其中x1、x2是方程x2-2x-8的两根,且x1<x2,过点A的直线l与抛物线只有一个公共点
(1)求A、C两点的坐标;
(2)求直线l的解析式;
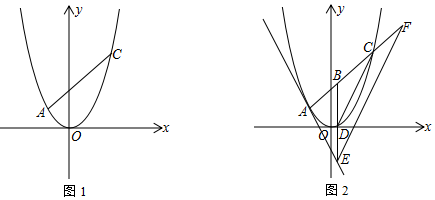
(3)如图2,点B是线段AC上的动点,若过点B作y轴的平行线BE与直线l相交于点E,与抛物线相交于点D,过点E作DC的平行线EF与直线AC相交于点F,求BF的长.
| 1 |
| 2 |
(1)求A、C两点的坐标;
(2)求直线l的解析式;
(3)如图2,点B是线段AC上的动点,若过点B作y轴的平行线BE与直线l相交于点E,与抛物线相交于点D,过点E作DC的平行线EF与直线AC相交于点F,求BF的长.

▼优质解答
答案和解析
(1)∵x1、x2是方程x2-2x-8的两根,且x12,
∴x1=-2,x2=4,
∴A(-2,2),C(4,8);
(2)设直线l的解析式为y=kx+b,
∵A(-2,2)在直线l上,
∴2=-2k+b,
∴b=2k+2,
∴直线l的解析式为y=kx+2k+2①,
∵抛物线y=
x2②,
联立①②化简得,x2-2kx-4k-4=0,
∵直线l与抛物线只有一个公共点,
∴△=(2k)2-4(-4k-4)=4k2+16k+16=4(k2+4k+4)=4(k+2)2=0,
∴k=-2,
∴b=2k+2=-2,
∴直线l的解析式为y=-2x-2;
(3)由(1)知,A(-2,2),C(4,8),
∴直线AC的解析式为y=x+4,
设点B(m,m+4),
∵(4.8),
∴BC=
|m-4|=
(4-m)
∵过点B作y轴的平行线BE与直线l相交于点E,与抛物线相交于点D,
∴D(m,
m2),E(m,-2m-2),
∴BD=m+4-
m2,BE=m+4-(-2m-2)=3m+6,
∵DC∥EF,
∴△BDC∽△BEF,
∴
=
,
∴
=
,
∴BF=6
.
∴x1=-2,x2=4,
∴A(-2,2),C(4,8);
(2)设直线l的解析式为y=kx+b,
∵A(-2,2)在直线l上,
∴2=-2k+b,
∴b=2k+2,
∴直线l的解析式为y=kx+2k+2①,
∵抛物线y=
| 1 |
| 2 |
联立①②化简得,x2-2kx-4k-4=0,
∵直线l与抛物线只有一个公共点,
∴△=(2k)2-4(-4k-4)=4k2+16k+16=4(k2+4k+4)=4(k+2)2=0,
∴k=-2,
∴b=2k+2=-2,
∴直线l的解析式为y=-2x-2;
(3)由(1)知,A(-2,2),C(4,8),
∴直线AC的解析式为y=x+4,
设点B(m,m+4),
∵(4.8),
∴BC=
| 2 |
| 2 |
∵过点B作y轴的平行线BE与直线l相交于点E,与抛物线相交于点D,
∴D(m,
| 1 |
| 2 |
∴BD=m+4-
| 1 |
| 2 |
∵DC∥EF,
∴△BDC∽△BEF,
∴
| BD |
| BE |
| BC |
| BF |
∴
m+4-
| ||
| 3m+6 |
| ||
| BF |
∴BF=6
| 2 |
看了 在平面直角坐标系中,抛物线y...的网友还看了以下:
两个向量不共线与共面说明什么问题l拉姆达等于0? 2020-03-30 …
高中数学双曲线与椭圆共焦点问题请问,双曲线与椭圆共焦点的情况下,椭圆的离心率与双曲线的离心率之间有 2020-05-16 …
直线系方程?圆系方程?共焦点的椭圆系,共渐近线的双曲线系?曲线系方程你知道吗?直线系方程?圆系方程 2020-05-16 …
直线与四边形的关系我们给出如下定义:如图1,当一条直线与一个四边形没有公共点时,我们称这条直线和这 2020-06-13 …
共渐近线的双曲线与共轭双曲线有区别吗,谢谢了哈哈哈 2020-07-13 …
异面直线与共面怎么区别我知道:不同在任何一个平面内的两条直线叫做异面直线.既不平行,也不相交.可我 2020-07-13 …
在平面直角坐标系中,有四条直线x=1,x=2,y=1,y=2围成的正方形ABCD(如图所示).(1 2020-07-29 …
高等数学中空间几何中俩直线共线与共面问题.已知:行列式:a1,b1,c1≠0a2,b2,c2a3. 2020-07-29 …
高二数学题已知长方体的一条对角线长的平方等于一个顶点上三条棱长的平方和,某长方体的一条对角线与共顶点 2021-01-09 …
长方体的一条对角线与共一个顶点的三个面所成的角分别为αβγ则cosα(平方)+cosβ(平方)+co 2021-01-10 …