早教吧作业答案频道 -->数学-->
如图,圆C:x2-(2+a)x+y2-ay+2a=0.(Ⅰ)若圆C与x轴相切,求圆C的方程;(Ⅱ)已知a>2,圆C与x轴相交于两点M,N(点M在点N的左侧).过点M任作一条直线与圆O:x2+y2=10相交于两点A,B.问
题目详情
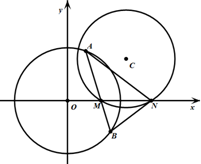
如图,圆C:x2-(2+a)x+y2-ay+2a=0.
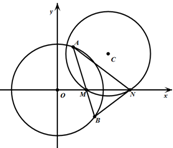
(Ⅰ)若圆C与x轴相切,求圆C的方程;
(Ⅱ)已知a>2,圆C与x轴相交于两点M,N(点M在点N的左侧).过点M任作一条直线与圆O:x2+y2=10相交于两点A,B.问:是否存在实数a,使得∠ANM=∠BNM?若存在,求出实数a的值,若不存在,请说明理由.

(Ⅰ)若圆C与x轴相切,求圆C的方程;
(Ⅱ)已知a>2,圆C与x轴相交于两点M,N(点M在点N的左侧).过点M任作一条直线与圆O:x2+y2=10相交于两点A,B.问:是否存在实数a,使得∠ANM=∠BNM?若存在,求出实数a的值,若不存在,请说明理由.
▼优质解答
答案和解析
(Ⅰ)由方程组
可得:x2-(2+a)x+2a=0,
由题意得△=(2+a)2-8a=(a-2)2=0,
所以a=2
故所求圆C的方程为C:x2-4x+y2-2y+4=0.
(Ⅱ)令y=0,得:x2-(2+a)x+2a=0,即(x-2)(x-a)=0.
所以M(2,0),N(a,0)…(5分)
假设存在实数a,
当直线AB与x轴不垂直时,
设直线AB的方程为:y=k(x-2),
代入x2+y2=10得,(1+k2)x2-4k2x+4k2-10=0,
设A(x1,y1),B(x2,y2),
则x1+x2=
,x1x2=
.
因为
+
=
而(x1-2)(x2-a)+(x2-2)(x1-a)=2x1x2-(a+2)(x1+x2)+4a=2•
-(a+2)
+4a=
,
因为∠ANM=∠BNM,
所以
+
=0,即
=0,得a=5.
当直线AB与x轴垂直时,也成立.
故存在a=5,使得∠ANM=∠BNM.
|

可得:x2-(2+a)x+2a=0,
由题意得△=(2+a)2-8a=(a-2)2=0,
所以a=2
故所求圆C的方程为C:x2-4x+y2-2y+4=0.
(Ⅱ)令y=0,得:x2-(2+a)x+2a=0,即(x-2)(x-a)=0.
所以M(2,0),N(a,0)…(5分)
假设存在实数a,
当直线AB与x轴不垂直时,
设直线AB的方程为:y=k(x-2),
代入x2+y2=10得,(1+k2)x2-4k2x+4k2-10=0,
设A(x1,y1),B(x2,y2),
则x1+x2=
| 4k2 |
| 1+k2 |
| 4k2-10 |
| 1+k2 |
因为
| y1 |
| x1-a |
| y2 |
| x2-a |
| k[(x1-2)(x2-a)+(x2-2)(x1-a)] |
| (x1-a)(x2-a) |
而(x1-2)(x2-a)+(x2-2)(x1-a)=2x1x2-(a+2)(x1+x2)+4a=2•
| 4k2-10 |
| 1+k2 |
| 4k2 |
| 1+k2 |
| 4a-20 |
| 1+k2 |
因为∠ANM=∠BNM,
所以
| y1 |
| x1-a |
| y2 |
| x2-a |
| 4a-20 |
| 1+k2 |
当直线AB与x轴垂直时,也成立.
故存在a=5,使得∠ANM=∠BNM.
看了 如图,圆C:x2-(2+a)...的网友还看了以下:
正方形ABCD和CEFG的边长分别为m,n,那么三角形AEG的面积的值( ) A 只与m的大小相关 2020-05-16 …
已知3x的n+1次方乘y的b-2次方与m乘x的平方合并同类项的结果是0,a,b,m各多少 2020-05-16 …
(一).等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上, 2020-06-05 …
如图,正方形ABCD和CEFG的边长分别为m、n,那么△AEG的面积的值()A.与m、n的大小都有 2020-06-14 …
对于同种物质而言,关于密度的公式“ρ=mv”下列说法正确的是()A.ρ与m成正比B.ρ与m、v没有 2020-06-27 …
如图,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时 2020-08-01 …
(2004•嘉兴)如图,等腰直角三角形ABC(∠C=90°)的直角边长与正方形MNPQ的边长均为4 2020-08-03 …
已知m的平方减mn=21,mn-n的平方=—12,求代数式m的平方-n的平方与m的平方-2mn+的平 2020-11-01 …
如图,等腰直角△ABC(∠C=90°)的直角边长与正方形MNPQ的边长均为6cm,CA与MN在同一直 2020-12-05 …
一带电圆盘水平放置中间有孔一带点小球从高处自由落下到盘上方M点时加速度为0那么运动到盘下方与M对称的 2021-01-09 …