早教吧作业答案频道 -->数学-->
如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.(1)求证:AE是⊙O的切线;(2)若AB=AD,AC=32,tan∠ADC=3,求BE的长.
题目详情
如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.
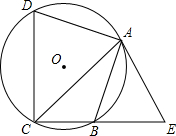
(1)求证:AE是⊙O的切线;
(2)若AB=AD,AC=3
,tan∠ADC=3,求BE的长.

(1)求证:AE是⊙O的切线;
(2)若AB=AD,AC=3
| 2 |
▼优质解答
答案和解析
(1)证明: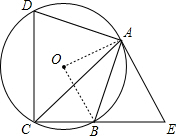
连接OA、OB,
∵∠ACB=45°,
∴∠AOB=2∠ACB=90°,
∵OA=OB,
∴∠OAB=∠OBA=45°,
∵∠BAE=45°,
∴∠OAE=45°+45°=90°,
∴OA⊥AE,
∵OA为半径,
∴AE是⊙O的切线;
(2) 过A作AF⊥CD于F,则∠AFC=∠AFD=90°,
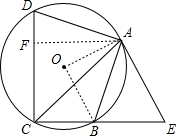
∵AB=AD,
∴
=
,
∴∠ACD=∠ACB=45°,
∵在Rt△AFC中,AC=3
,∠ACF=45°,
∴AF=FC=AC•sin∠ACF=3,
∵在Rt△AFD中,tan∠ADC=
=3,
∴DF=1,
∴AB=AD=
=
,且CD=CF+DF=4,
∵四边形ABCD内接⊙O,
∴∠ABE=∠CDA,
∵∠BAE=∠DCA,
∴△ABE∽△CDA,
∴
=
,
∴
=
,
∴BE=
.

连接OA、OB,
∵∠ACB=45°,
∴∠AOB=2∠ACB=90°,
∵OA=OB,
∴∠OAB=∠OBA=45°,
∵∠BAE=45°,
∴∠OAE=45°+45°=90°,
∴OA⊥AE,
∵OA为半径,
∴AE是⊙O的切线;
(2) 过A作AF⊥CD于F,则∠AFC=∠AFD=90°,

∵AB=AD,
∴
 |
| AB |
 |
| AD |
∴∠ACD=∠ACB=45°,
∵在Rt△AFC中,AC=3
| 2 |
∴AF=FC=AC•sin∠ACF=3,
∵在Rt△AFD中,tan∠ADC=
| AF |
| DF |
∴DF=1,
∴AB=AD=
| 32+12 |
| 10 |
∵四边形ABCD内接⊙O,
∴∠ABE=∠CDA,
∵∠BAE=∠DCA,
∴△ABE∽△CDA,
∴
| BE |
| DA |
| AB |
| CD |
∴
| BE | ||
|
| ||
| 4 |
∴BE=
| 5 |
| 2 |
看了 如图,已知四边形ABCD内接...的网友还看了以下:
1.a≠0,b≠0,则a/|a|+b/|b|的不同取值的个数为()A.3B.2C.1D.02.若|x 2020-03-31 …
设集合A={1,a,b},B={a,a^2,ab}且A=B,求实数A,B的值因为集合需要满足互异性 2020-05-15 …
已知A={1,2,a},B={1,a的二次方},A∪B={1,2,a},求所有可能的a值已知A={ 2020-06-02 …
1.在三角形abc中,证明a/b-b/a=c(CosB/b-CosA/a)2.在三角形abc中,已 2020-07-21 …
集合的运算1.已知A={1,2,3,4},B={3,4,5},求A交集B,A并集B.2.已知A={ 2020-07-30 …
已知椭圆X^2/a^2+y^2/b^2=1(a>b>0)的3个项的顶点分别为B1(0,-b)B2( 2020-08-01 …
集合A(-1,1),集合B(b-a,a+b),a=1是A交B的充分条件,求b的范围求高手们快帮帮小 2020-08-02 …
已知正数abc,且a/b+c=b/c+a=c/a+b=k.则在下列四个点中,在正比例函数y=kx图像 2020-11-01 …
定义运算a*b=a(1-b),下面给出了几个结论:1.a*b=b*a2.若a+b=0,则(a*a)+ 2020-11-08 …
近世代数2、设A,B是U的子集,规定A+B=(A-B)(B-A).证明:(1)A+B=B+A(2)A 2020-11-28 …