早教吧作业答案频道 -->数学-->
在△ABC中,BC=8,高AH为4,△DEF在△ABC内,三个顶点D、E、F分别在BC、AB和AC上,且点D与点A在直线EF的异侧,我们称△DEF为△ABC的内接三角形.(1)如图1,当△DEF∽△ABC,且EF=3时,求△DEF的
题目详情
在△ABC中,BC=8,高AH为4,△DEF在△ABC内,三个顶点D、E、F分别在BC、AB和AC上,且点D与点A在直线EF的异侧,我们称△DEF为△ABC的内接三角形.
(1)如图1,当△DEF∽△ABC,且EF=3时,求△DEF的面积;
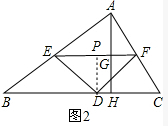
(2)如图2,在△ABC的内接△DEF中,DE=DF,∠EDF=90°,且EF∥BC,EF与AH交于G点,求△DEF的面积;
(3)如图3,在△ABC的内接三角形DEF中,DE=DF,且EF∥BC,EF与AH交于G点,求等腰△DEF面积的最大值.
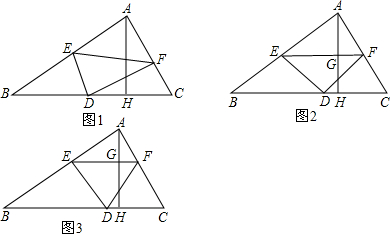
(1)如图1,当△DEF∽△ABC,且EF=3时,求△DEF的面积;
(2)如图2,在△ABC的内接△DEF中,DE=DF,∠EDF=90°,且EF∥BC,EF与AH交于G点,求△DEF的面积;
(3)如图3,在△ABC的内接三角形DEF中,DE=DF,且EF∥BC,EF与AH交于G点,求等腰△DEF面积的最大值.

▼优质解答
答案和解析
 (1)∵BC=8,高AH为4,
(1)∵BC=8,高AH为4,
∴△ABC的面积为
×8×4=16,
∵△DEF∽△ABC,
∴
=(
)2,
∴△DEF的面积为:
;
(2)如图2,作DP⊥EF于P,
∵DE=DF,∠EDF=90°,
∴PD=
EF,
由题意可知,四边形PDHG为矩形,∴PD=GH,
设EF=x,则PD=GH=
x,
∵EF∥BC,
∴
=
,即
=
,
解得,x=4,
∴△DEF的面积=
×EF×PD=4;
(3)如图2,设EF=a,
∵EF∥BC,
∴
=
,即
=
,
解得,GH=4-
a,
∵PD=GH,
∴△DEF面积=
×a×(4-
a)=-
(a-4)2+4,
∵-
<0,
∴等腰△DEF面积的最大值为4.
 (1)∵BC=8,高AH为4,
(1)∵BC=8,高AH为4,∴△ABC的面积为
| 1 |
| 2 |
∵△DEF∽△ABC,
∴
| △DEF的面积 |
| △ABC的面积 |
| EF |
| BC |
∴△DEF的面积为:
| 9 |
| 4 |
(2)如图2,作DP⊥EF于P,
∵DE=DF,∠EDF=90°,
∴PD=
| 1 |
| 2 |
由题意可知,四边形PDHG为矩形,∴PD=GH,
设EF=x,则PD=GH=
| 1 |
| 2 |
∵EF∥BC,
∴
| EF |
| BC |
| AG |
| AH |
| x |
| 8 |
4-
| ||
| 4 |
解得,x=4,
∴△DEF的面积=
| 1 |
| 2 |
(3)如图2,设EF=a,
∵EF∥BC,
∴
| EF |
| BC |
| AG |
| AH |
| a |
| 8 |
| 4-GH |
| 4 |
解得,GH=4-
| 1 |
| 2 |
∵PD=GH,
∴△DEF面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵-
| 1 |
| 2 |
∴等腰△DEF面积的最大值为4.
看了 在△ABC中,BC=8,高A...的网友还看了以下:
在锐角△ABC中,a,b,c,分别为角A,B,C所对的边,又c=根号21,b=4,且BC边上的高h= 2020-03-30 …
在锐角△ABC中,a.b.c分别为角A.B.C所对的边,又c=√21b=4且BC边上的高h=2√3. 2020-03-30 …
1.在△ABC中,三个内角A,B,C的对边分别是a,b,c若a=2,b=4,C=60°,试解△AB 2020-04-27 …
在锐角△ABC中,a,b,c分别为角A,B,C所对的边,又c=根号21,b=4且AB边上的高为h= 2020-05-22 …
在锐角△ABC中,a,b,c分别为角A,B,C所对的边,又c=根号21,b=4且BC边上的高为h= 2020-05-22 …
初二的函数题,在平面直角坐标系中,点O是坐标原点.已知等腰梯形OABC,OA//BC,点A(4,0 2020-06-06 …
某一矿井的示意图如图2——16所示以地面为准,A点的高度是+4米,BC两点的高度分别是-15米与- 2020-06-13 …
从山顶A望地面C.D俩点1.计算:(√sin^2*75°-4sin75°cos60°+1)+(si 2020-07-15 …
三角网算方量问题:A点标高为255.34;B点为254.87;C点为257.23;AB距离为8.4 2020-07-19 …
几道简单的高二数学题(直线方程)1.(1)已知三角形的顶点是A(8,5),B(4,-2),C(-6 2020-08-01 …