函数f（x）=Asin（2x+φ）（|φ|≤π2，A>0）部分图象如图所示，且f（a）=f（b）=0，对不同的x1，x2∈[a，b]，若f（x1）=f（x2），有f（x1+x2）=3，则（）A.f（x）在（-5π12，π12）上是减函数B.

Question

函数f（x）=Asin（2x+φ）（|φ|≤

(π)/(2)，A>0）部分图象如图所示，且f（a）=f（b）=0，对不同的x₁，x₂∈[a，b]，若f（x₁）=f（x₂），有f（x₁+x₂）=√(3)，则（　　）

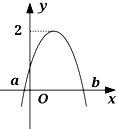
A. f（x）在（-

(5π)/(12)，(π)/(12)）上是减函数

B. f（x）在（-

(5π)/(12)，(π)/(12)）上是增函数

C. f（x）在（

(π)/(3)，(5π)/(6)）上是减函数

D. f（x）在（

(π)/(3)，(5π)/(6)）上是增函数

Answer 1

∵f（x）=Asin（2x+φ），∴函数最小正周期为T=π；
由图象得A=2，且f（a）=f（b）=0，
∴(1)/(2)•(2π)/(ω)=b-a，解得b-a=(π)/(2)；
又x₁，x₂∈[a，b]，且f（x₁）=f（x₂）时，有f（x₁+x₂）=√(3)，
∴sin[2（x₁+x₂）+φ]=(√(3))/(2)，即2（x₁+x₂）+φ=(2π)/(3)，
且sin（2•(x1+x2)/(2)+φ）=1，即2•(x1+x2)/(2)+φ=(π)/(2)，
解得φ=(π)/(3)，
∴f（x）=2sin（2x+(π)/(3)）；
令-(π)/(2)+2kπ≤2x+(π)/(3)≤(π)/(2)+2kπ，k∈Z，
∴-(5π)/(6)+2kπ≤2x≤(π)/(6)+2kπ，k∈Z，
解得-(5π)/(12)+kπ≤x≤(π)/(12)+kπ，k∈Z，
∴函数f（x）在区间[-(5π)/(12)+kπ，(π)/(12)+kπ]，k∈Z上是单调增函数，
∴f（x）在区间（-(5π)/(12)，(π)/(12)）上是单调增函数．
故选：B．