如图，已知一次函数y1=kx+b的图象与反比例函数y2=4x的图象交于点A（-4，m），且与y轴交于点B，第一象限内点C在反比例函数y2=4x的图象上，且以点C为圆心的圆与x轴，y轴分别相切于点D，B（1）

Question

如图，已知一次函数y₁=kx+b的图象与反比例函数y₂=(4)/(x)的图象交于点A（-4，m），且与y轴交于点B，第一象限内点C在反比例函数y₂=(4)/(x)的图象上，且以点C为圆心的圆与x轴，y轴分别相切于点D，B

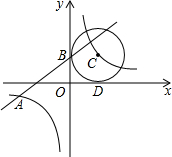
（1）求m的值；
（2）求一次函数的表达式；
（3）根据图象，当y₁<y₂<0时，写出x的取值范围．

Answer 1

（1）把点A（-4，m）的坐标代入y₂=(4)/(x)，
则m=(4)/(-4)=-1，
得m=-1；

（2）连接CB，CD，
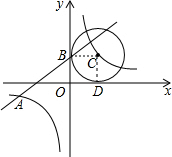∵ C与x轴，y轴相切于点D，B，
∴∠CBO=∠CDO=90°=∠BOD，BC=CD，
∴四边形BODC是正方形，
∴BO=OD=DC=CB，
∴设C（a，a）代入y₂=(4)/(x)得：a²=4，
∵a>0，∴a=2，
∴C（2，2），B（0，2），
把A（-4，-1）和（0，2）的坐标代入y₁=kx+b中，
得：

-4k+b=-1

b=2

，
解得：

k=(3)/(4)

b=2

，
∴一次函数的表达式为：y₁=(3)/(4)x+2；

（3）∵A（-4，-1），
∴当y₁<y₂<0时，x的取值范围是：x<-4．