如图，已知在正方形ABCD中，点O为对角线AC的中点，过O点的射线OM、ON分别交AB、BC于点E、F，且∠EOF=90°，BO、EF交于点P，则下面结论中：①图形中全等的三角形只有三对；②△EOF是等腰直角三

Question

如图，已知在正方形ABCD中，点O为对角线AC的中点，过O点的射线OM、ON分别交AB、BC于点E、F，且∠EOF=90°，BO、EF交于点P，则下面结论中：
①图形中全等的三角形只有三对；②△EOF是等腰直角三角形；
③正方形ABCD的面积等于四边形OEBF面积的4倍；
④BE+BF=

√(2)OA；⑤AE²+BE²=2OP•OB．
正确结论的个数是（　　）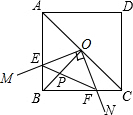

A. 4个

B. 3个

C. 2个

D. 1个

Answer 1

①不正确；
图形中全等的三角形有四对：△ABC≌△ADC，△AOB≌△COB，△AOE≌△BOF，△BOE≌△COF；理由如下：
∵四边形ABCD是正方形，
∴AB=BC=CD=DA，∠BAD=∠ABC=∠BCD=∠D=90°，∠BAO=∠BCO=45°，
在△ABC和△ADC中，

AB=AD	amp;
BC=DC	amp;
AC=AC	amp;

，
∴△ABC≌△ADC（SSS）；
∵点O为对角线AC的中点，
∴OA=OC，
在△AOB和△COB中，

OA=OC	amp;
AB=CB	amp;
OB=OB	amp;

，
∴△AOB≌△COB（SSS）；
∵AB=CB，OA=OC，∠ABC=90°，
∴∠AOB=90°，∠OBC=45°，
又∵∠EOF=90°，
∴∠AOE=∠BOF，
在△AOE和△BOF中，

∠OAE=∠OBF=45°	amp;
OA=OB	amp;
∠AOE=∠BOF	amp;

，
∴△AOE≌△BOF（ASA）；
同理：△BOE≌△COF；
②正确；理由如下：
∵△AOE≌△BOF，
∴OE=OF，
∴△EOF是等腰直角三角形；
③正确．理由如下：
∵△AOE≌△BOF，
∴四边形OEBF的面积=△ABO的面积=(1)/(4)正方形ABCD的面积；
④正确．理由如下：
∵△BOE≌△COF，
∴BE=CF，
∴BE+BF=CF+BF=BC=AB=√(2)OA；
⑤正确．理由如下：
∵△AOE≌△BOF，
∴AE=BF，
∴AE²+CF²=BE²+BF²=EF²=2OF²，
在△OPF与△OFB中，
∠OBF=∠OFP=45°，
∠POF=∠FOB，
∴△OPF∽△OFB，
∴OP：OF=OF：OB，
∴OF²=OP•OB，
∴AE²+CF²=20P•OB．
正确结论的个数有4个；
故选：A．