如图，已知∠AOB=90°，以O为顶点、OB为一边画∠BOC，然后再分别画出∠AOC与∠BOC的平分线OM、ON．（1）在图1中，射线OC在∠AOB的内部．①若锐角∠BOC=30°，则∠MON=°；②若锐角∠BOC=n&d

Question

如图，已知∠AOB=90°，以O为顶点、OB为一边画∠BOC，然后再分别画出∠AOC与∠BOC的平分线OM、ON．
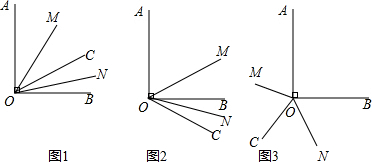
（1）在图1中，射线OC在∠AOB的内部．
①若锐角∠BOC=30°，则∠MON=___°；
②若锐角∠BOC=n°，则∠MON=___°．
（2）在图2中，射线OC在∠AOB的外部，且∠BOC为任意锐角，求∠MON的度数．
（3）在（2）中，“∠BOC为任意锐角”改为“∠BOC为任意钝角”，其余条件不变，（图3），求∠MON的度数．

Answer 1

（1）①∵∠AOB=90°，∠BOC=30°，
∴∠AOC=60°，
∵OM，ON分别平分∠AOC，∠BOC，
∴∠COM=(1)/(2)∠AOC，∠CON=(1)/(2)∠BOC，
∴∠MON=∠COM+∠CON=(1)/(2)∠AOB=45°，
故答案为：45°，
②∵∠AOB=90°，∠BOC=n°，
∴∠AOC=（90-n）°，
∵OM，ON分别平分∠AOC，∠BOC，
∴∠COM=(1)/(2)∠AOC=(1)/(2)（90-n）°，∠CON=(1)/(2)∠BOC=(1)/(2)n°，
∴∠MON=∠COM+∠CON=(1)/(2)∠AOB=45°，
故答案为：45°；
（2）∵∠AOB=90°，设∠BOC=α，
∴∠AOC=90°+α，
∵OM，ON分别平分∠AOC，∠BOC，
∴∠COM=(1)/(2)∠AOC，∠CON=(1)/(2)∠BOC，
∴∠MON=∠COM-∠CON=(1)/(2)∠AOB=45°，
（3）∵OM，ON分别平分∠AOC，∠BOC，
∴∠COM=(1)/(2)∠AOC，∠CON=(1)/(2)∠BOC，
∴∠MON=∠COM+∠CON=(1)/(2)（∠AOC+∠BOC）=(1)/(2)（360°-90°）=135°．