早教吧作业答案频道 -->数学-->
已知:直线AB与CD相交于点O.(Ⅰ)如图1,若∠AOM=90°,OC平分∠AOM,则∠AOD=.(Ⅱ)如图2,若∠AOM=90°,∠BOC=4∠BON,OM平分∠CON,求∠MON的大小;(Ⅲ)如图3,若∠AOM=α,∠BOC=4∠B
题目详情
已知:直线AB与CD相交于点O.
(Ⅰ)如图1,若∠AOM=90°,OC平分∠AOM,则∠AOD=___.
(Ⅱ)如图2,若∠AOM=90°,∠BOC=4∠BON,OM平分∠CON,求∠MON的大小;
(Ⅲ)如图3,若∠AOM=α,∠BOC=4∠BON,OM平分∠CON,求∠MON的大小(用含α的式子表示).
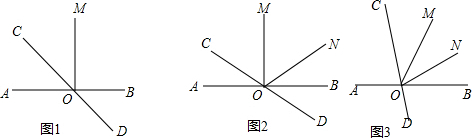
(Ⅰ)如图1,若∠AOM=90°,OC平分∠AOM,则∠AOD=___.
(Ⅱ)如图2,若∠AOM=90°,∠BOC=4∠BON,OM平分∠CON,求∠MON的大小;
(Ⅲ)如图3,若∠AOM=α,∠BOC=4∠BON,OM平分∠CON,求∠MON的大小(用含α的式子表示).

▼优质解答
答案和解析
解(1)∵∠AOM=90°,OC平分∠AOM,
∴∠AOC=
∠AOM=
×90°=45°,
∵∠AOC+∠AOD=180°,
∴∠AOD=180°-∠AOC=180°-45°=135°,
即∠AOD的度数为135°;
(2)∵∠BOC=4∠NOB
∴设∠NOB=x°,∠BOC=4x°,
∴∠CON=∠COB-∠BON=4x°-x°=3x°,
∵OM平分∠CON,
∴∠COM=∠MON=
∠CON=
x°,
∵∠BOM=
x+x=90°,
∴x=36°,
∴∠MON=
x°=
×36°=54°,
即∠MON的度数为54°;
(3)∵∠BOC=4∠NOB
∴设∠NOB=x°,∠BOC=4x°,
∴∠CON=∠COB-∠BON=4x°-x°=3x°,
∵OM平分∠CON,
∴∠COM=∠MON=
∠CON=
x°,
∵∠BOM=
x+x=α,
∴x=
α,
∴∠MON=
×
α=
α.
∴∠AOC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOC+∠AOD=180°,
∴∠AOD=180°-∠AOC=180°-45°=135°,
即∠AOD的度数为135°;
(2)∵∠BOC=4∠NOB
∴设∠NOB=x°,∠BOC=4x°,
∴∠CON=∠COB-∠BON=4x°-x°=3x°,
∵OM平分∠CON,
∴∠COM=∠MON=
| 1 |
| 2 |
| 3 |
| 2 |
∵∠BOM=
| 3 |
| 2 |
∴x=36°,
∴∠MON=
| 3 |
| 2 |
| 3 |
| 2 |
即∠MON的度数为54°;
(3)∵∠BOC=4∠NOB
∴设∠NOB=x°,∠BOC=4x°,
∴∠CON=∠COB-∠BON=4x°-x°=3x°,
∵OM平分∠CON,
∴∠COM=∠MON=
| 1 |
| 2 |
| 3 |
| 2 |
∵∠BOM=
| 3 |
| 2 |
∴x=
| 2 |
| 5 |
∴∠MON=
| 3 |
| 2 |
| 2 |
| 5 |
| 3 |
| 5 |
看了 已知:直线AB与CD相交于点...的网友还看了以下:
如图,等腰三角形ABC中,以腰AB为直径的⊙O交底边BC于点D,交AC于点E,连接DE.(1)求证 2020-04-27 …
O、A、B、C为空间四个点,又OA、OB、OC为空间的一个基底,则()A.O、A、B、C四点不共线 2020-05-14 …
如图,在△ABC中,以AB为直径作⊙O交BC于点D,DE交AC于E.(1)若AB=AC,DE⊥AC 2020-05-16 …
已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧AD上取一点E使∠EBC=∠DEC,延 2020-06-23 …
如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.(1)求证:A 2020-06-27 …
如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的⊙O交AC于点E,点D是BC边的中点, 2020-07-09 …
如图2-6-26已知以AF为直径的⊙O与以OA为直径的⊙O1内切于A△ADF内接于⊙ODB⊥FA于 2020-07-31 …
直线l:y=mx-m+1(m为常数,且m≠0)与坐标轴交于A、B两点,若△AOB(O是原点)的面积恰 2020-11-01 …
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E点F在AC的延长线上,且 2020-11-03 …
如图,圆O是三角形ABC的外接圆,AB是圆O的直径,D是AB延长线上的一点AE⊥DC交DC的延长线于 2020-11-20 …