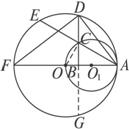
如图2-6-26已知以AF为直径的⊙O与以OA为直径的⊙O1内切于A△ADF内接于⊙ODB⊥FA于B交⊙O1于C连结AC并延长交⊙O于E求证:(1)AC=CE;(2)AC2=DB2-BC2.图2-6-26

Question

如图 2-6-26 已知以AF为直径的⊙O与以OA为直径的⊙O ₁ 内切于A △ADF内接于⊙O DB⊥FA于B交⊙O ₁ 于C 连结AC并延长交⊙O于E 求证:

(1)AC=CE;

(2)AC ² =DB ² -BC ² .

图 2-6-26

Answer 1

思路分析:要证AC ² =DB ² -BC ² 将其化为等积式.

由(1)及平方差公式有AC·CE=(DB+BC)(DB-BC)=(DB+BC)·DC.

考虑利用相交弦定理.

证明:(1)连结OC 因OA是⊙O ₁ 的直径 则OC⊥AE.

∴AC=CE.

(2)延长DB交⊙O于G.

∵DB⊥AF ∴DB=BG.

由相交弦定理有AC·CE=CG·CD=(BG+BC)(DB-BC)=(DB+BC)(DB-BC)

=DB ² -BC ² .

∵AC=CE ∴AC ² =DB ² -BC ² .