早教吧作业答案频道 -->数学-->
已知∠AOD=α,射线OB、OC在∠AOD的内部,OM平分∠AOC,ON平分∠BOD.(1)如图1,当射线OB与OC重合时,求∠MON的大小;(2)在(1)的条件下,若射线OC绕点O逆时针旋转一定角度θ,如图2,求∠
题目详情
已知∠AOD=α,射线OB、OC在∠AOD的内部,OM平分∠AOC,ON平分∠BOD.
(1)如图1,当射线OB与OC重合时,求∠MON的大小;
(2)在(1)的条件下,若射线OC绕点O逆时针旋转一定角度θ,如图2,求∠MON的大小;
(3)在(2)的条件下,射线OC绕点O继续逆时针旋转,旋转到与射线OA的反向延长线重合为止,在这一旋转过程中,∠MON=___.
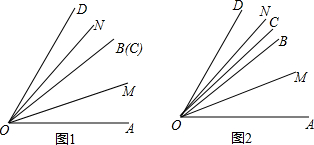
(1)如图1,当射线OB与OC重合时,求∠MON的大小;
(2)在(1)的条件下,若射线OC绕点O逆时针旋转一定角度θ,如图2,求∠MON的大小;
(3)在(2)的条件下,射线OC绕点O继续逆时针旋转,旋转到与射线OA的反向延长线重合为止,在这一旋转过程中,∠MON=___.

▼优质解答
答案和解析
(1)∵OM平分∠AOB,ON平分∠BOD,
∴∠BOM=
∠AOB,∠BON=
∠BOD,
∴∠MON=∠COM+∠BON-∠BOC=
(∠AOC+∠BOD),
∵∠AOD=∠AOB+∠BOD=α,
∴∠MON=
α;
(2)∵OM平分∠AOC,ON平分∠BOD.
∴∠COM=
∠AOC,∠BON=
∠BOD,
∴∠MON=∠COM+∠BON-∠BOC=
(∠AOC+∠BOD)-∠BOC,
∵∠AOD=∠AOC+∠BOD-∠BOC=α,
∴∠AOC+∠BOD=α+θ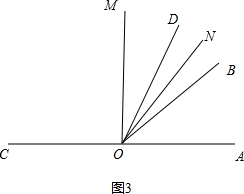 ,
,
∴∠MON=
(α+θ)-θ=
(α-θ);
(3)如图3,∵OM平分∠AOC,ON平分∠BOD.
∴∠AOM=
∠AOC=90°,∠DON=
∠BOD,
∴∠MON=90°-α+
∠BOD,
∵∠AOD-∠BOD+BOC=180°,
∴∠BOD=α+θ-180°,
∴∠MON=90°-α+
∠BOD=90°-α+
(α+θ-180°)=
(θ-α).
故答案为
(θ-α).
∴∠BOM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠COM+∠BON-∠BOC=
| 1 |
| 2 |
∵∠AOD=∠AOB+∠BOD=α,
∴∠MON=
| 1 |
| 2 |
(2)∵OM平分∠AOC,ON平分∠BOD.
∴∠COM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠COM+∠BON-∠BOC=
| 1 |
| 2 |
∵∠AOD=∠AOC+∠BOD-∠BOC=α,
∴∠AOC+∠BOD=α+θ
 ,
,∴∠MON=
| 1 |
| 2 |
| 1 |
| 2 |
(3)如图3,∵OM平分∠AOC,ON平分∠BOD.
∴∠AOM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=90°-α+
| 1 |
| 2 |
∵∠AOD-∠BOD+BOC=180°,
∴∠BOD=α+θ-180°,
∴∠MON=90°-α+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
看了 已知∠AOD=α,射线OB、...的网友还看了以下:
已知a,b,c分别为三角形ABC三个内角A,B,C的对边acosC+根号3asinC-b-c=o. 2020-04-05 …
由H,C,O,Na三种元素按要求写出化学式(1)由H,C,O,Na四种元素按要求写出化学式气体单质 2020-05-02 …
在共点O三条不共面直线a,b,c上,在点O两侧分别取点A和A',B和B',C和C',且AO=A'O 2020-05-13 …
已知:如图,在直角坐标系中,直角三角形OAB,O为坐标原点,AB=1,OB=3,将△OAB绕着A点 2020-05-13 …
如图,已知角A、O、B=90°,角B、O、C=30°,OM平分角AOC,ON平分角B、O、C.1. 2020-06-18 …
平行四边形ABCO四个定点坐标分别是A(√3,√3)B(3√3,√3)C(2√3,0)O(0,0) 2020-07-30 …
已知abc≠0,且a+b+c=o,求a*(1/b+1/c)+b(1/c+1/a)+c(1/a+1/b 2020-11-01 …
已知O(0,0),A(2,1),O,A,B,C依逆时针方向构成正方形的四个顶点.(1)求B,C两点的 2020-12-21 …
已知a+b+c=o求证(a+b)的三次方+(b+c)的三次方+(c+a)的三次方-3abc=o 2021-01-05 …
已知a,b,c分别为三角形ABC三个内角A,B,C的对边acosC+根号3asinC-b-c=o.求 2021-02-07 …