如图，C为射线AB上一点，AB=30，AC比BC的多5，P，Q两点分别从A，B两点同时出发．分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动，运动时间为t秒，M为BP的中点，N为QM的中点，以下结

Question

如图，C为射线AB上一点，AB=30，AC比BC的多5，P，Q两点分别从A，B两点同时出发．分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动，运动时间为t秒，M为BP的中点，N为QM的中点，以下结论：
①BC=2AC；②AB=4NQ；③当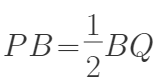时，t=12，其中正确结论的个数是（　　）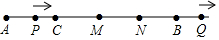
               

A. 0

B. 1

C. 2

D. 3

Answer 1

设BC=x，
∴AC=(1)/(4)x+5
∵AC+BC=AB
∴x+(1)/(4)x+5=30，
解得：x=20，
∴BC=20，AC=10，
∴BC=2AC，故①成立，
∵AP=2t，BQ=t，
当0≤t≤15时，
此时点P在线段AB上，
∴BP=AB-AP=30-2t，
∵M是BP的中点
∴MB=(1)/(2)BP=15-t
∵QM=MB+BQ，
∴QM=15，
∵N为QM的中点，
∴NQ=(1)/(2)QM=(15)/(2)，
∴AB=4NQ，
当15<t≤30时，
此时点P在线段AB外，且点P在Q的左侧，
∴AP=2t，BQ=t，
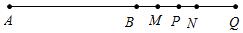
∴BP=AP-AB=2t-30，
∵M是BP的中点
∴BM=(1)/(2)BP=t-15
∵QM=BQ-BM=15，
∵N为QM的中点，
∴NQ=(1)/(2)QM=(15)/(2)，
∴AB=4NQ，
当t>30时，
此时点P在Q的右侧，
∴AP=2t，BQ=t，
∴BP=AP-AB=2t-30，
∵M是BP的中点
∴BM=(1)/(2)BP=t-15
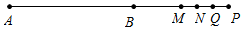
∵QM=BQ-BM=15，
∵N为QM的中点，
∴NQ=(1)/(2)QM=(15)/(2)，
∴AB=4NQ，
综上所述，AB=4NQ，故②正确，
当0<t≤15，PB=(1)/(2)BQ时，此时点P在线段AB上，
∴AP=2t，BQ=t
∴PB=AB-AP=30-2t，
∴30-2t=(1)/(2)t，
∴t=12，
当15<t≤30，PB=(1)/(2)BQ时，此时点P在线段AB外，且点P在Q的左侧，
∴AP=2t，BQ=t，
∴PB=AP-AB=2t-30，
∴2t-30=(1)/(2)t，
t=20，
当t>30时，此时点P在Q的右侧，
∴AP=2t，BQ=t，
∴PB=AP-AB=2t-30，
∴2t-30=(1)/(2)t，
t=20，不符合t>30，
综上所述，当PB=(1)/(2)BQ时，t=12或20，故③错误；
故选（C）