早教吧作业答案频道 -->数学-->
已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA,EC.(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;(2)如图2,若点P在线段AB的中点,
题目详情
已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA,EC.
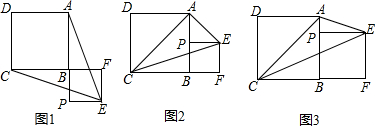
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)如图2,若点P在线段AB的中点,连接AC,判断△ACE的形状,并说明理由;
(3)如图3,若点P在线段AB上,连接AC,当EP平分∠AEC时,设AB=a,BP=b,求a:b及∠AEC的度数.

(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)如图2,若点P在线段AB的中点,连接AC,判断△ACE的形状,并说明理由;
(3)如图3,若点P在线段AB上,连接AC,当EP平分∠AEC时,设AB=a,BP=b,求a:b及∠AEC的度数.
▼优质解答
答案和解析
证明:(1)∵四边形ABCD和四边形BPEF是正方形,
∴AB=BC,BP=BF,
∴AP=CF,
在△APE和△CFE中,
∵
,
∴△APE≌△CFE,
∴EA=EC;
(2)△ACE是直角三角形,理由是:
如图2,∵P为AB的中点,
∴PA=PB,
∵PB=PE,
∴PA=PE,
∴∠PAE=45°,
又∵∠BAC=45°,
∴∠CAE=90°,即△ACE是直角三角形;
(3)设CE交AB于G,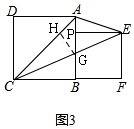
∵EP平分∠AEC,EP⊥AG,
∴AP=PG=a-b,BG=a-(2a-2b)=2b-a,
∵PE∥CF,
∴
=
,即
=
,
解得:a=
b,
∴a:b=
:1,
作GH⊥AC于H,
∵∠CAB=45°,
∴HG=
AG=
(2
b-2b)=(2-
)b,
又∵BG=2b-a=(2-
)b,
∴GH=GB,GH⊥AC,GB⊥BC,
∴∠HCG=∠BCG,
∵PE∥CF,
∴∠PEG=∠BCG,
∴∠AEC=∠ACB=45°.
∴AB=BC,BP=BF,
∴AP=CF,
在△APE和△CFE中,
∵
|
∴△APE≌△CFE,
∴EA=EC;
(2)△ACE是直角三角形,理由是:
如图2,∵P为AB的中点,
∴PA=PB,
∵PB=PE,
∴PA=PE,
∴∠PAE=45°,
又∵∠BAC=45°,
∴∠CAE=90°,即△ACE是直角三角形;
(3)设CE交AB于G,

∵EP平分∠AEC,EP⊥AG,
∴AP=PG=a-b,BG=a-(2a-2b)=2b-a,
∵PE∥CF,
∴
| PE |
| BC |
| PG |
| GB |
| b |
| a |
| a-b |
| 2b-a |
解得:a=
| 2 |
∴a:b=
| 2 |
作GH⊥AC于H,
∵∠CAB=45°,
∴HG=
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |
又∵BG=2b-a=(2-
| 2 |
∴GH=GB,GH⊥AC,GB⊥BC,
∴∠HCG=∠BCG,
∵PE∥CF,
∴∠PEG=∠BCG,
∴∠AEC=∠ACB=45°.
看了 已知正方形ABCD,P为射线...的网友还看了以下:
关于图中,各点地理位置说法正确的是()A.A点45°E,30°NB.B点120°W,60°NC.D 2020-05-13 …
(2012•黄石模拟)关于图中,各点地理位置说法正确的是()A.A点45°E,30°NB.B点12 2020-05-13 …
光速是最快的速度光速D点到E点距离为100,A为观察1B为观察2,c是运动1,c1在c里,在D点时 2020-05-15 …
线y=-1/2x+2交y轴于A点且与直线y=x交于B点.在x轴上存在一动点Q(t,0),过Q点作x 2020-05-22 …
(2010•河源)如图,直角梯形OABC中,OC∥AB,C(0,3),B(4,1),以BC为直径的 2020-07-21 …
如图,点p为∠ABC角平分线上一点,D点和E点分别在AB和BC上,且PD=PE过P作PF⊥AB于F 2020-07-21 …
(2010•河源)如图,直角梯形OABC中,OC∥AB,C(0,3),B(4,1),以BC为直径的 2020-07-22 …
如图,真空中M、N处放置两等量异号电荷,a、b、c表示电场中的3条等势线,d点和e点位于等势线a上 2020-07-30 …
一个半径为10厘米,中心角为135度的扇形,D点、E点是弧BC的三等分点,那么阴影部分的面积为多少 2020-08-01 …
如下图,点P为∠ABC角平分线上的一点,D点和E点分别在AB和BC上,且PD=PE,试探究∠BDP 2020-08-03 …