早教吧作业答案频道 -->物理-->
通过探究得到弹性势能的表达式为Ep=12kx2，式中k为弹簧的劲度系数，x为弹簧伸长（或缩短）的长度．请利用弹性势能的表达式计算下列问题：放在地面上的物体上端系在劲度系数k=200N/m的弹
题目详情
通过探究得到弹性势能的表达式为Ep=
kx2，式中k为弹簧的劲度系数，x为弹簧伸长（或缩短）的长度．请利用弹性势能的表达式计算下列问题：
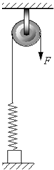
放在地面上的物体上端系在劲度系数k=200N/m的弹簧上，弹簧的另一端拴在跨过定滑轮的绳子上，如图所示．手拉右侧绳子的另一端，当拉力往下做功为4J时，物体开始离开地面，继续拉绳再做功32J，使物体缓慢升高到离地一定高度处，如果不计弹簧重和滑轮跟绳的摩擦，求：
（1）弹簧的弹性势能；
（2）右侧绳端总共下降的高度．
| 1 |
| 2 |
放在地面上的物体上端系在劲度系数k=200N/m的弹簧上，弹簧的另一端拴在跨过定滑轮的绳子上，如图所示．手拉右侧绳子的另一端，当拉力往下做功为4J时，物体开始离开地面，继续拉绳再做功32J，使物体缓慢升高到离地一定高度处，如果不计弹簧重和滑轮跟绳的摩擦，求：
（1）弹簧的弹性势能；
（2）右侧绳端总共下降的高度．
▼优质解答
答案和解析
（1）弹簧的弹性势能为：Ep=WF=4J
（2）由Ep=
kx2得：x=0.2m
物体离地后：W2=Fh=mgh
而mgh=kx
联立得：h=0.8m
综上，右侧绳端总共下降的高度为：h总=x+h=1m
答：（1）弹簧的弹性势能是4J；
（2）右侧绳端总共下降的高度是1m．
（2）由Ep=
| 1 |
| 2 |
物体离地后：W2=Fh=mgh
而mgh=kx
联立得：h=0.8m
综上，右侧绳端总共下降的高度为：h总=x+h=1m
答：（1）弹簧的弹性势能是4J；
（2）右侧绳端总共下降的高度是1m．
看了 通过探究得到弹性势能的表达式...的网友还看了以下：
已知函数f(x)=lnx+1/x+ax.其中x>0,常数a∈R.已知函数f(x)=lnx+1/x+ 2020-05-13 …
已知函数f(x)=(x∧2-3x+9/4)e∧x其中e为自然数的底数.(1)函数f(x)的图像在x 2020-06-03 …
已知函数f(x)=(ax^2+bx+c)e^x,其中e为自然数对数的底数,a,b,c为常数,若函数 2020-06-08 …
若函数f(x)在R上可导,且f(x)＞f'(x),当a>b时,下列不等式成立的是A.e^af(若函 2020-07-29 …
设函数f(x)=alnx-bx^2(x>0)(1)若函数f(x)在x=1处与直线y=-1/2相切， 2020-07-31 …
已知函数f(x)=(x^2+ax+a)e^(-x）（a为常数,e为自然对数的底）.（1）若函数已知 2020-08-02 …
已知a>0,函数f(x)=e^x/a+a/e^x在R上满足f(-x)=f(x),其中e为自然对数的 2020-08-02 …
已知a∈R,函数f(x)=e^x+a|x-2|.（1）当0＜a≤e时,若函数f(x)在区间［1,+∞ 2020-12-03 …
已知a属于R,函数f(x)=x分之a+lnx-1,g(x=(lnx-1)e的x次方+x(其中为自然对 2020-12-08 …
已知函数f(x)=e^x-2x+a有零点,则实数a的取值范围为?令e^x-2x+a=0则a=2x-e 2020-12-26 …