早教吧作业答案频道 -->数学-->
如图,已知二次函数y=ax2+4x+c的图象经过点A(1,-1)和点B(-3,-9).(1)求该二次函数的表达式;(2)写出该抛物线的对称轴及顶点M坐标;(3)点P(m,-m)与点Q均在该函数图象上(其
题目详情
如图,已知二次函数y=ax2+4x+c的图象经过点A(1,-1)和点B(-3,-9).
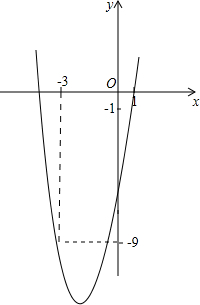
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点M坐标;
(3)点P(m,-m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离.
(4)求△MPQ的面积.

(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点M坐标;
(3)点P(m,-m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离.
(4)求△MPQ的面积.
▼优质解答
答案和解析
(1)∵二次函数y=ax2+4x+c的图象经过点A(1,-1)和点B(-3,-9),
∴
,
解得:
,
∴该二次函数的表达式为y=x2+4x-6;
(2)∵y=x2+4x-6
=x2+4x+4-4-6
=(x+2)2-10,
∴该抛物线的对称轴为直线x=-2,
顶点坐标为(-2,-10);
(3)∵点P(m,-m)在函数图象上(m>0),
∴m2+4m-6=-m,
整理得m2+5m-6=0,
解得m1=1,m2=-6(舍去),
∴点P的坐标为(1,-1),
∵点P、Q关于抛物线的对称轴x=-2对称,
设点Q坐标为(x,-1),
∴
=-2,
∴x=-5,
∴点Q坐标为(-5,-1),
∴点Q到x轴距离为1.
(4)∵PQ∥x轴,
∴PQ=1-(-5)=6
点M到直线PQ距离h为:-1-(-10)=9
∴S△MPQ=
×PQ×h,
=
×6×9,
=27.
答:△MPQ的面积为27.
∴
|
解得:
|
∴该二次函数的表达式为y=x2+4x-6;
(2)∵y=x2+4x-6
=x2+4x+4-4-6
=(x+2)2-10,
∴该抛物线的对称轴为直线x=-2,
顶点坐标为(-2,-10);
(3)∵点P(m,-m)在函数图象上(m>0),
∴m2+4m-6=-m,
整理得m2+5m-6=0,
解得m1=1,m2=-6(舍去),
∴点P的坐标为(1,-1),
∵点P、Q关于抛物线的对称轴x=-2对称,
设点Q坐标为(x,-1),
∴
| 1+x |
| 2 |
∴x=-5,
∴点Q坐标为(-5,-1),
∴点Q到x轴距离为1.
(4)∵PQ∥x轴,
∴PQ=1-(-5)=6
点M到直线PQ距离h为:-1-(-10)=9
∴S△MPQ=
| 1 |
| 2 |
=
| 1 |
| 2 |
=27.
答:△MPQ的面积为27.
看了 如图,已知二次函数y=ax2...的网友还看了以下:
1.等腰三角形的两个底角相等(简称“等边对等角),画图并写出已知求证再写出证明过程.2.等腰三角形 2020-04-07 …
设无向图G=(y,E),其中y={l,2,3,4,5},E={(1,2,4),(2,5,5),(1 2020-04-25 …
从一条山路的山下到山顶,走1小时还差1千米;从山顶道山下,50分钟可以走完.已知下山的速度是上山的 2020-05-13 …
已知抛物线y=ax^2+bx+c经过点A(-1,4)B(5,4)且与y轴的交点的纵坐标为3/2(1 2020-06-21 …
数学题目甲市有8千顶帐篷乙市有6千顶帐篷现在要往A和B地运送甲市有8千顶帐篷乙市有6千顶帐篷现在要 2020-07-01 …
写出下面各句运用的描写方法.1.他顶不过二十岁,长得矮矮的,写出下面各句运用的描写方法.1.他顶不 2020-07-07 …
如何计算承台顶相对标高和底板相对标高?地下室已知底板绝对标高为0.3,承台顶已知绝对标高为-1.2 2020-07-21 …
我市某企业地震灾区捐助价值26万元的甲,乙两种帐篷共300三百顶,已知甲种帐篷每顶800元,乙种帐每 2020-11-12 …
关于初中几何证明格式规范问题1.因为旋转翻折平移的全等怎么写因为所以2.对于相似三角形的规范步骤3. 2020-12-02 …
已知f(x)是二次函数且满足f(0)=1f(x+1)=f(x)-2x+2求f(x)解析式已知f(x) 2020-12-08 …