早教吧作业答案频道 -->数学-->
如图所示,四边形MNPQ为圆内接四边形,对角线MP与NQ相交于点S,R为MN与QP延长线的交点,且MN=NP,∠MPQ=60°,△MPR为等腰三角形.(Ⅰ)求∠PQM的大小;(Ⅱ)若MN=3,求QM的长.
题目详情
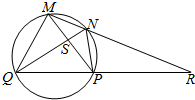
如图所示,四边形MNPQ为圆内接四边形,对角线MP与NQ相交于点S,R为MN与QP延长线的交点,且MN=NP,∠MPQ=60°,△MPR为等腰三角形.
(Ⅰ)求∠PQM的大小;
(Ⅱ)若MN=3,求QM的长.

(Ⅰ)求∠PQM的大小;
(Ⅱ)若MN=3,求QM的长.
▼优质解答
答案和解析
(Ⅰ)∵MN=NP,∴∠NMP=∠NPM,
∵△MPR为等腰三角形,PM=PR,∴∠NMP=∠R
∵∠MPQ=60°,
∴∠PMR=∠R=30°,
∴∠PQM=∠MQN+∠NQP=∠MPN+∠NMP=60°;
(Ⅱ)∵MN=NP,
∴∠NPM=30°,
∵∠MPQ=60°,∴∠NPQ=90°,
∴PQ=3tan60°=3
∵MN=3,
∴MP=2×3×
=3
,
∵∠MPQ=60°,
∴QM=3
.
∵△MPR为等腰三角形,PM=PR,∴∠NMP=∠R
∵∠MPQ=60°,
∴∠PMR=∠R=30°,
∴∠PQM=∠MQN+∠NQP=∠MPN+∠NMP=60°;
(Ⅱ)∵MN=NP,
∴∠NPM=30°,
∵∠MPQ=60°,∴∠NPQ=90°,
∴PQ=3tan60°=3
| 3 |
∵MN=3,
∴MP=2×3×
| ||
| 2 |
| 3 |
∵∠MPQ=60°,
∴QM=3
| 3 |
看了 如图所示,四边形MNPQ为圆...的网友还看了以下:
a=(Q+2,Q²-COS²w) b=(m,m/2+sinw) q w m均为实数 若a=2b 求 2020-05-16 …
数轴上有三个动点P,Q,M数轴上有三个动点P,Q,M,P表示的数是-12,Q表示的数是0,M表示的 2020-06-06 …
设一组初始记录关键字序列为(Q,H,C,Y,P,A,M,S,R,D,F,X),则按字母升序的第一趟 2020-07-17 …
设全集U,集合P.Q.M是U的子集,M≠空集,则P真包含于Q的一个充分非必要条件是()A.Q真包含 2020-07-29 …
(2014•安徽模拟)如图所示,电荷Q均匀分布在半径为R的球面上,在球壳上任取一小圆片B,Q′点是 2020-07-31 …
如图,PQ⊥MQ,NM⊥MQ,Q,M分别为垂足,点A是线段MQ上(不包括端点)的动点,连结PA,过点 2020-11-02 …
有这么一道题(截取下来的):q是质数,1/q+2/q+...+(q-1)/q=m为什么答案分析那里写 2020-11-20 …
matlab模拟带电粒子在均匀电磁场中的运动functionydot=ddlzfun(t,y,fla 2020-12-14 …
着急、数学集合!已知集合A={a+b√2|a∈Q,b∈Q},m∈A,n∈A求证:m*n∈A已知集合A 2020-12-19 …
英语翻译数学集合论问题(英语)LetZ2bethesetofallpairsofintegers.D 2020-12-23 …