如图，C为∠A0B的边0A上一点，OC=6，N为边OB上异于点O的一动点，P是线段CN上一点，过点P分别作PQ∥OA交0B于点Q，PM∥OB交OA于点M．（1）若OM=4，OQ=1，求QN的长；（2）当点N在边OB上运动时，四边

Question

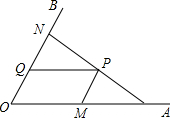
如图，C为∠A0B的边0A上一点，OC=6，N为边OB上异于点O的一动点，P是线段CN上一点，过点P分别作PQ∥OA交0B于点Q，PM∥OB交OA于点M．

（1）若OM=4，OQ=1，求QN的长；
（2）当点N在边OB上运动时，四边形OMPQ始终保持为菱形．问：(1)/(OM)-(1)/(ON)的值是否发生变化？如果变化，求出其取值范围；如果不变，请说明理由．

Answer 1

（1）∵PQ∥OA，PM∥OB，
∴四边形OMPQ是平行四边形，
∴PQ=OM=4，PM=OQ=1，
∴CM=OC-OM=2，
∵PQ∥OA，PM∥OB，
∴∠NPQ=∠PCN，∠NQP=∠O=∠PMC，
∴△NPQ∽△CPM，
∴(PQ)/(CM)=(NQ)/(PM)，
∴(4)/(2)=(NQ)/(1)，
∴NQ=2；

（2）(1)/(OM)-(1)/(ON)的值不发生变化，理由如下：
设OM=x，ON=y，
∵四边形OMPQ为菱形，
∴OQ=QP=OM=x，NQ=y-x，
∵PQ∥OA，
∴∠NQP=∠O，
又∵∠QNP=∠ONC，
∴△NQP∽△NOC，
∴(QP)/(OC)=(NQ)/(ON)，即(x)/(6)=(y-x)/(y)，
∴6y-6x=xy，
两边都除以6xy，得(1)/(x)-(1)/(y)=(1)/(6)，即(1)/(OM)-(1)/(ON)=(1)/(6)．