早教吧作业答案频道 -->数学-->
如图,面积为6的平行四边形纸片ABCD中,AB=3,∠BAD=45°,按下列步骤裁剪和拼图.第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD
题目详情
如图,面积为6的平行四边形纸片ABCD中,AB=3,∠BAD=45°,按下列步骤裁剪和拼图.
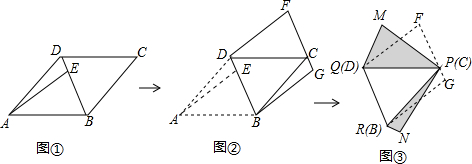
第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).
则由纸片拼成的五边形PMQRN中,BD=___,对角线MN长度的最小值为___.

第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).
则由纸片拼成的五边形PMQRN中,BD=___,对角线MN长度的最小值为___.
▼优质解答
答案和解析
∵△ABE≌△CDF≌△PMQ,
∴AE=DF=PM,∠EAB=∠FDC=∠MPQ,
∵△ADE≌△BCG≌△PNR,
∴AE=BG=PN,∠DAE=∠CBG=∠RPN,
∴PM=PN,
∵四边形ABCD是平行四边形,
∴∠DAB=∠DCB=45°,
∴∠MPN=90°,
∴△MPN是等腰直角三角形,
当PM最小时,对角线MN最小,即AE取最小值,
∴当AE⊥BD时,AE取最小值,
过D作DF⊥AB于F,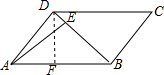
∵平行四边形ABCD的面积为6,AB=3,
∴DF=2,
∵∠DAB=45°,
∴AF=DF=2,
∴BF=1,
∴BD=
=
,
∴AE=
=
=
,
∴MN=
AE=
.
故答案为:
,
.
∴AE=DF=PM,∠EAB=∠FDC=∠MPQ,
∵△ADE≌△BCG≌△PNR,
∴AE=BG=PN,∠DAE=∠CBG=∠RPN,
∴PM=PN,
∵四边形ABCD是平行四边形,
∴∠DAB=∠DCB=45°,
∴∠MPN=90°,
∴△MPN是等腰直角三角形,
当PM最小时,对角线MN最小,即AE取最小值,
∴当AE⊥BD时,AE取最小值,
过D作DF⊥AB于F,

∵平行四边形ABCD的面积为6,AB=3,
∴DF=2,
∵∠DAB=45°,
∴AF=DF=2,
∴BF=1,
∴BD=
| DF2+BF2 |
| 5 |
∴AE=
| DF•AB |
| BD |
| 2×3 | ||
|
6
| ||
| 5 |
∴MN=
| 2 |
6
| ||
| 5 |
故答案为:
| 5 |
6
| ||
| 5 |
看了 如图,面积为6的平行四边形纸...的网友还看了以下:
这个是必要条件还是充要条件“A=B”是“是直线Y=X+2与圆(X-A)^2+(Y-B)^2=2相切 2020-04-26 …
如图所示,L形木板A放在固定的表面粗糙的斜面上,滑块B至于木板上表面,若A B 一起沿如图所示,L 2020-05-17 …
怎么判断向量是否共面?例如下面这题需要判断选项中的项量是否共面:若{a,b,c}构成空间的一个基底 2020-06-22 …
若a,b是空间两条不相交的直线,a属于平面α,b属于平面β,且α‖β,a,b的距离为h1,α,β的 2020-06-27 …
a,b是异面直线,()A,若P为不在a,b上的一点,则过点p有且只有一个平面与a,b平行B,过直线 2020-07-22 …
如图已知直线a在平面α内,直线b在平面α内,a∥b,直线c∥平面α,a与c是异面直线,求证b,c是 2020-08-02 …
异面直线上的平行,过异面直线a,b有几个平面使a,b到他的距离相等?我的空间想象能力有限,过任意两 2020-08-02 …
关于球的问题1球O半径为1,A,B,C都在球面上,A,B与A,C的球面距离为派/4,B,C的球面距 2020-08-02 …
a,b为一面直线,则下列结论正确的是()A过不在a,b上的任一点,可做一个平面与a,b平行B过不在a 2020-12-23 …
求A,B,C三个图形的公共部分的面积?A.b.c分别代表面积为10.11.13的三张不同行状的纸片, 2021-01-15 …