早教吧作业答案频道 -->数学-->
如图,在∠ABC内有一点M.(1)分别画出点M关于OA、0B的对称点M1、M2,连接M1M2,交0A于点P,交OB于点Q;(2)在(1)的条件下,若M1M2=10cm,则△MPQ的周长为cm;若∠A0B=50°,则∠M1OM2=
题目详情
如图,在∠ABC内有一点M.
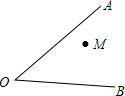
(1)分别画出点M关于OA、0B的对称点M1、M2,连接M1M2,交0A于点P,交OB于点Q;
(2)在(1)的条件下,若M1M2=10cm,则△MPQ的周长为___cm;若∠A0B=50°,则∠M1OM2=___;
(3)在OA、OB上分别任取点P′、Q′(不与点P、Q重合),连接MP′、P′Q′、MQ′,得到△MP′Q′,比较△MP′Q与△MPQ的周长,你得到什么结论?

(1)分别画出点M关于OA、0B的对称点M1、M2,连接M1M2,交0A于点P,交OB于点Q;
(2)在(1)的条件下,若M1M2=10cm,则△MPQ的周长为___cm;若∠A0B=50°,则∠M1OM2=___;
(3)在OA、OB上分别任取点P′、Q′(不与点P、Q重合),连接MP′、P′Q′、MQ′,得到△MP′Q′,比较△MP′Q与△MPQ的周长,你得到什么结论?
▼优质解答
答案和解析
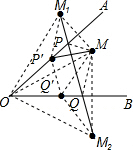 (1)如图所示:
(1)如图所示:
(2)∵点M关于OA,0B的对称点M1,M2,
∴M1P=PM,QM=QM2,
∴△MPQ的周长等于M1P+PQ+M2Q=M1M2=10cm;
∵MM1关于直线OA对称,MM2关于直线OB对称,
∴∠M1OM+∠M1OM=∠AOB=50°,
∴∠M1OM2=100°.
故答案为:10,100;
(3)如图所示:由△MPQ的周长等于M1M2,则此时△MPQ的周长面积最小,
△MP′Q′的周长为:M1P′+P′Q′+Q′M2,
故△MP′Q′大于△MPQ的周长
 (1)如图所示:
(1)如图所示:(2)∵点M关于OA,0B的对称点M1,M2,
∴M1P=PM,QM=QM2,
∴△MPQ的周长等于M1P+PQ+M2Q=M1M2=10cm;
∵MM1关于直线OA对称,MM2关于直线OB对称,
∴∠M1OM+∠M1OM=∠AOB=50°,
∴∠M1OM2=100°.
故答案为:10,100;
(3)如图所示:由△MPQ的周长等于M1M2,则此时△MPQ的周长面积最小,
△MP′Q′的周长为:M1P′+P′Q′+Q′M2,
故△MP′Q′大于△MPQ的周长
看了 如图,在∠ABC内有一点M....的网友还看了以下:
十万火急,若点P(1,-1)在直线y=ax+b(a,b∈R),求点(a,b)满足的不等式 2020-06-29 …
一、我们知道1/1×2=1/1-1/2=1/2,1/2×3=1/2-1/3=1/6验证:1/3×4 2020-07-17 …
已知椭圆方程x²/4+y²=1.(2)过点P(1,1/4)的直线与椭圆交于两点D,E,若DP=PE 2020-07-18 …
直角三角形1:1:根号2请问各路高手:直角三角形三个角分别为30°60°90°我想问的是:1:1: 2020-07-22 …
寻找规律解数学题1/1*2=1-1/22/2*3=1/2-1/31/3*4=1/3-1/4……计算 2020-07-22 …
已知直线l的方程为3x-4y+1=0,点p(1,1)在直线l上,写出直线l的参数方程 2020-07-30 …
已知抛物线C:y=ax^2,p(1,-1)在抛物线C上,过点P作斜率为K1,K2的两条直线,分别交 2020-07-31 …
P(n)推导已知p(1)=1;p(n)=(1-1/(n^2))p(n-1)+2/n-1/(n^2) 2020-08-01 …
(1)在一个平面上画一组间距为d=4cm的平行线,将一根长度为l=3cm的针任意投掷在这个平面上, 2020-08-01 …
由下列各式:1>1/2,1+1/2+1/3>1有下列各式:1>1/2;1+1/2+1/3>1;1+1 2020-10-30 …