早教吧作业答案频道 -->数学-->
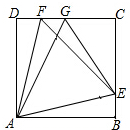
已知,四边形ABCD为正方形,E,F分别在BC,CD上,△AEF为等边三角形,G为CD上一点,EG平分∠AGC,求证:AG=FG+EG.
题目详情
已知,四边形ABCD为正方形,E,F分别在BC,CD上,△AEF为等边三角形,G为CD上一点,EG平分∠AGC,求证:AG=FG+EG.

▼优质解答
答案和解析
证明:如图延长GC使得GM=GA,连接AM,EM,AM交EG于O,在GA上截取GK=FG,连接FK.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠D=∠B=∠DCB=90°,
∵△AEF是等边三角形,
∴AE=AF=EF,∠EAF=∠AEF=∠AFE=60°,
∵EG平分∠AGC,
∴GE垂直平分AM,
∴EA=EM=EF,
在RT△ADF和RT△ABE中,
,
∴△ADF≌△ABE,
∴DF=BE,CF=CE,
∴∠EFC=∠FEC=∠EMF=45°,
∵∠GAM=∠GMA,∠EAM=∠EMA,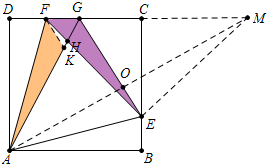
∴∠GAE=∠EMG=45°=∠GFH,
∵∠GFH+∠FHG+∠FGH=180°,∠HAE+∠AEH+∠AHE=180°,∠FHG=∠EHA,
∴∠FGH=∠AEF=60°,
∴∠AEG=∠EGC=60°,
∵GK=FG,∠FGK=60°,
∴△FGK是等边三角形,
∴FK=FG=GK,∠GFK=∠AFE=60°,
∴∠AFK=∠EFG,
在△AFK和△EFG中,
,
∴△AFK≌△EFG,
∴AK=EG,
∴AG=AK+GK=GE+GF.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠D=∠B=∠DCB=90°,
∵△AEF是等边三角形,
∴AE=AF=EF,∠EAF=∠AEF=∠AFE=60°,
∵EG平分∠AGC,
∴GE垂直平分AM,
∴EA=EM=EF,
在RT△ADF和RT△ABE中,
|
∴△ADF≌△ABE,
∴DF=BE,CF=CE,
∴∠EFC=∠FEC=∠EMF=45°,
∵∠GAM=∠GMA,∠EAM=∠EMA,

∴∠GAE=∠EMG=45°=∠GFH,
∵∠GFH+∠FHG+∠FGH=180°,∠HAE+∠AEH+∠AHE=180°,∠FHG=∠EHA,
∴∠FGH=∠AEF=60°,
∴∠AEG=∠EGC=60°,
∵GK=FG,∠FGK=60°,
∴△FGK是等边三角形,
∴FK=FG=GK,∠GFK=∠AFE=60°,
∴∠AFK=∠EFG,
在△AFK和△EFG中,
|
∴△AFK≌△EFG,
∴AK=EG,
∴AG=AK+GK=GE+GF.
看了 已知,四边形ABCD为正方形...的网友还看了以下:
线性代数证明,设A是n阶方阵,且A的平方等于En,证明R(A+E)+R(A-E)设A是n阶方阵,且 2020-04-05 …
n阶矩阵A满足A^2=A时称A为幂等函数设A为幂等函数证明A+E和E-2A是可逆矩阵并求其逆 2020-04-12 …
已知向量a≠e,|e|=1,满足:任意t∈R.已知向量a不等于e,|e|=1,对任意t属于R,恒有 2020-07-25 …
若函数f(x)在R上可导,且f(x)>f'(x),当a>b时,下列不等式成立的是A.e^af(若函 2020-07-29 …
矩阵分配律(A-E)(A+E)=(A+E)(A-E),因为两边的乘积都为A^2-E^2,不是在矩阵 2020-07-31 …
若关于x的不等式ex-(a+1)x-b≥0(e为自然对数的底数)在R上恒成立,则(a+1)b的最大 2020-08-01 …
设A为可逆矩阵,则存在有限个初等矩阵P1,P2.PL,使A=P1P2.PL.我想问证明过程中说因A 2020-08-02 …
数学向量1,A,B,C,D为平面上4个互异点,且满足(向量DB+DC-2DA)点乘(AB-AC)=0 2020-11-02 …
.设A,B是任意的n阶方阵,(A-E)(A+E)=(A+E)(A-E)为什么相等 2020-11-02 …
设n阶方阵A满足A*A=E,|A+E|不等于0,证明:A=E. 2020-11-02 …