早教吧作业答案频道 -->数学-->
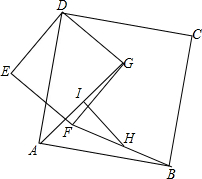
已知四边形ABCD,四边形DEFG都是正方形,H是BF中点,I是AG中点,求证:AG=2HI.
题目详情
已知四边形ABCD,四边形DEFG都是正方形,H是BF中点,I是AG中点,求证:AG=2HI.

▼优质解答
答案和解析
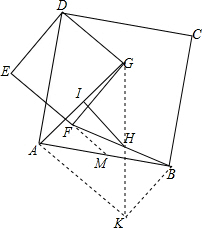 证明:连接GH并延长至K,令GH=HK,延长EF交AB于M,连接AK,BK,
证明:连接GH并延长至K,令GH=HK,延长EF交AB于M,连接AK,BK,
在△FGH和△BKH中
∵
,
∴△FGH≌△BKH(SAS),
∴∠GFH=∠KBH,FG=BK=DG,
设∠MFB=α,∠FBM=β,
∴∠EMA=∠MFB+∠FBM=α+β,
∵∠DEM=∠DAB=90°,
∴∠EMA=∠EDA=α+β,
∴∠ADG=90°-∠EDA=90°-α-β,
∵∠GFM=90°,∴∠GFH=90°-α=∠KBH,
∴∠ABK=∠KBH-∠FBM=90°-α-β=∠ADG,
在△ADG和△ABK中
∵
,
∴△ADG≌△ABK(SAS),
∴AG=AK,
∵I为AG中点,H为GK中点,由中位线可知:IH=
AK=
AG,
∴AG=2HI.
 证明:连接GH并延长至K,令GH=HK,延长EF交AB于M,连接AK,BK,
证明:连接GH并延长至K,令GH=HK,延长EF交AB于M,连接AK,BK,在△FGH和△BKH中
∵
|
∴△FGH≌△BKH(SAS),
∴∠GFH=∠KBH,FG=BK=DG,
设∠MFB=α,∠FBM=β,
∴∠EMA=∠MFB+∠FBM=α+β,
∵∠DEM=∠DAB=90°,
∴∠EMA=∠EDA=α+β,
∴∠ADG=90°-∠EDA=90°-α-β,
∵∠GFM=90°,∴∠GFH=90°-α=∠KBH,
∴∠ABK=∠KBH-∠FBM=90°-α-β=∠ADG,
在△ADG和△ABK中
∵
|
∴△ADG≌△ABK(SAS),
∴AG=AK,
∵I为AG中点,H为GK中点,由中位线可知:IH=
| 1 |
| 2 |
| 1 |
| 2 |
∴AG=2HI.
看了 已知四边形ABCD,四边形D...的网友还看了以下:
△ABC中,AB=AC,AD是底边BC上的高,DE⊥AC于E,G是DE的中点,AG,BE相交于点H 2020-05-13 …
已知:如图,在△ABC中,D、E、F分别为三边中点,AG是BC边上的高,求证:四边形DGEF是等腰 2020-05-21 …
已知:如图,在△ABC中,D、E、F分别为三边中点,AG是BC边上的高,求证:四边形DGEF是等腰 2020-05-21 …
已知:如图,在△ABC中,D、E、F分别为三边中点,AG是BC边上的高,求证:四边形DGEF是等腰 2020-06-02 …
我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.(1)如图1,四边形AB 2020-06-13 …
各图形的中点四边形1.矩形的中点四边形2.菱形的中点四边形3.正方形的中点四边形4.四边形的中点四 2020-06-13 …
四边形ABCD中,点E、F、G、H分别为AB、BC、CD、DA边的中点,顺次连接各边中点得到的新四 2020-07-30 …
如图,H是△ABC的边BC的中点,AG平分∠BAC,点D是AC上一点,且AG⊥BD于点G.已知AB 2020-07-30 …
已知:如图,在△ABC中,D、E、F分别为三边中点,AG是BC边上的高,求证:四边形DGEF是等腰 2020-07-30 …
(2012•孝感)我们把依次连接任意一个四边形各边中点得到的四边形叫做中点四边形.如图,在四边形AB 2020-11-12 …