早教吧作业答案频道 -->数学-->
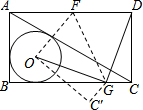
如图,AC是矩形ABCD的对角线,O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG,点F,G分别在AD,BC上,连结OG,DG,若OG⊥DG,且O的半径长为1,则BC+AB的值
题目详情
如图,AC是矩形ABCD的对角线, O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG,点F,G分别在AD,BC上,连结OG,DG,若OG⊥DG,且 O的半径长为1,则BC+AB的值___.

▼优质解答
答案和解析
如图所示:设圆0与BC的切点为M,连接OM.
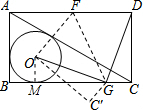
∵BC是圆O的切线,M为切点,
∴OM⊥BC.
∴∠OMG=∠GCD=90°.
由翻折的性质可知:OG=DG.
∵OG⊥GD,
∴∠OGM+∠DGC=90°.
又∵∠MOG+∠OGM=90°,
∴∠MOG=∠DGC.
在△OMG和△GCD中,
,
∴△OMG≌△GCD.
∴OM=GC=1.
CD=GM=BC-BM-GC=BC-2.
∵AB=CD,
∴BC-AB=2.
设AB=a,则BC=a+2.
∵圆O是△ABC的内切圆,
∴AC=AB+BC-2r.
∴AC=2a.
∴
=
.
∴∠ACB=30°.
∴
=
,即
=
.
解得:a=
+1.
∴AB=
+1,BC=AB+2=
+3.
所有AB+BC=4+2
.
故答案为:4+2
.

∵BC是圆O的切线,M为切点,
∴OM⊥BC.
∴∠OMG=∠GCD=90°.
由翻折的性质可知:OG=DG.
∵OG⊥GD,
∴∠OGM+∠DGC=90°.
又∵∠MOG+∠OGM=90°,
∴∠MOG=∠DGC.
在△OMG和△GCD中,
|
∴△OMG≌△GCD.
∴OM=GC=1.
CD=GM=BC-BM-GC=BC-2.
∵AB=CD,
∴BC-AB=2.
设AB=a,则BC=a+2.
∵圆O是△ABC的内切圆,
∴AC=AB+BC-2r.
∴AC=2a.
∴
| AB |
| AC |
| 1 |
| 2 |
∴∠ACB=30°.
∴
| AB |
| BC |
| ||
| 3 |
| a |
| a+2 |
| ||
| 3 |
解得:a=
| 3 |
∴AB=
| 3 |
| 3 |
所有AB+BC=4+2
| 3 |
故答案为:4+2
| 3 |
看了 如图,AC是矩形ABCD的对...的网友还看了以下:
如图所示,以平面镜的高度为直径作一圆,使圆所在的平面与平面镜垂直,在圆周上有三个发光点a、b、c跟 2020-05-13 …
p{font-size:10.5pt;line-height:150%;margin:0;padd 2020-05-14 …
回答下列问题:1.如果线段AB绕点O旋转360度,点A的轨迹与点B的诡计完全一样,试判断点O的位置 2020-05-16 …
对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离不大于这个圆的半径,那么称图形A被 2020-06-08 …
如图所示,小圆筒A底部有一个半径为r的圈孔,大圆筒B套于A的外部,里外圆筒中分别盛有密度为ρ1和ρ 2020-06-17 …
如图所示,一个半径R为0.6m的光滑半圆细环竖直放置并固定在水平桌面上,O为圆心,A为半圆环如图所 2020-06-22 …
如图甲所示,在同一平面内有两个相互绝缘的金属圆环A、B,圆环A平分圆环B为面积相等的两部分,当圆环 2020-07-01 …
所示,以平面镜的高度为直径作一圆,使圆所在的平面与平面镜垂直,在圆周上有三个发光点a、b、c,若a 2020-07-05 …
如图甲,R0为定值电阻,两金属圆环固定在同一绝缘平面内.左端连接在一周期为T0的正弦交流电源上,经二 2020-11-08 …
(2010•保定一模)如图,A、B、C分别表示面积为9、10、11的三个圆.已知三个圆所覆盖的总面积 2020-11-12 …