早教吧作业答案频道 -->数学-->
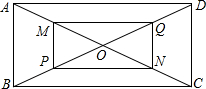
已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,点M,P,N,Q分别在AO,BO,CO,DC上,且AM=BP=CN=DQ.求证:四边形MPNQ是矩形.
题目详情
已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,点M,P,N,Q分别在AO,BO,CO,DC上,且AM=BP=CN=DQ.求证:四边形MPNQ是矩形.

▼优质解答
答案和解析
∵四边形ABCD是矩形,
∴∠ABC=90°;AC=BD,AO=
AC,BO=
BD;
∴AO=BO;而AM=BP,
∴AM:AO=BP:BO,
∴MP∥AB;同理可证:QN∥CD;
∵AB∥CD,
∴MP∥QN;同理可证:MQ∥PN,
∴四边形MPNQ是平行四边形;
∵MP∥AB,PN∥BC,∠ABC=90°,
∴∠MPN=90°,
∴四边形MPNQ是矩形.
∴∠ABC=90°;AC=BD,AO=
| 1 |
| 2 |
| 1 |
| 2 |
∴AO=BO;而AM=BP,
∴AM:AO=BP:BO,
∴MP∥AB;同理可证:QN∥CD;
∵AB∥CD,
∴MP∥QN;同理可证:MQ∥PN,
∴四边形MPNQ是平行四边形;
∵MP∥AB,PN∥BC,∠ABC=90°,
∴∠MPN=90°,
∴四边形MPNQ是矩形.
看了 已知:如图,在矩形ABCD中...的网友还看了以下:
已知an=2n,令bn=λq^(an)+λ(λ,q为常数,q>0且q≠1),Cn=3+n+(b1+ 2020-04-27 …
数列{an}是以a为着项,q为公比的等比数列,令bn=1-a1-a2-a3-…-an,Cn=2-b 2020-05-13 …
关于微分的几何意义,通常看到这样的表达:"设Δx是曲线y = f(x)上的点M的在横坐标上的增量, 2020-05-16 …
数学排列组合题!作对就采纳!1.求证Cn+2^m=Cn^m+2Cn^m-1+Cn^m-22.(1) 2020-07-01 …
如图,正方形ABCD中,M为AD边上的一点,连接BM,过点C作CN∥BM,交AD的延长线于点N,在 2020-07-07 …
如图1,在△ABC中,∠B=60°,点M从点B出发沿射线BC方向,在射线BC上运动.在点M运动的过 2020-07-27 …
在f(m,n)中,.m.n.f(m,n)均为非负整数且对任意的m,n有f(0,n)=n+1,f(m 2020-07-31 …
一道求证题(与二项式定理有关)C10(0)*C20(20)+C10(1)*C20(1)+…+C10( 2020-10-31 …
二项式的有关..已知组合数Cn^m对任意的有意义的m都成立,求n的值要能听懂的躲不起啊我写错啦题;C 2020-11-07 …
已知数列{an}的前n项和为Sn,且满足Sn=2an-n若bn=log2(an+1),在bk(k为下 2020-11-19 …