早教吧作业答案频道 -->数学-->
如图,四边形ABCD中,∠ADC的角平分线DE与∠BCD的角平分线CA相交于E点,DE交BC于点F,连结AF,已知∠ACD=32°,∠CDE=58°.(1)求证:AD∥BC;(2)当AD=5,DE=3时,求CE的长度.
题目详情
如图,四边形ABCD中,∠ADC的角平分线DE与∠BCD的角平分线CA相交于E点,DE交BC于点F,连结AF,已知∠ACD=32°,∠CDE=58°.
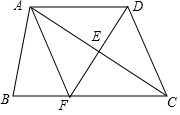
(1)求证:AD∥BC;
(2)当AD=5,DE=3时,求CE的长度.

(1)求证:AD∥BC;
(2)当AD=5,DE=3时,求CE的长度.
▼优质解答
答案和解析
(1)∵DE平分∠ADC,CA平分∠BCD,
∴∠ADC=2∠CDE=116°,∠BCD=2∠ACD=64°
∵∠ADC+∠BCD=116°+64°=180°
∴AD∥BC;
(2)∵∠DCC=180°-∠ACD-∠CDE=90°,
∴DF⊥AC,
在△DAE和△DEC中
,
∴△DAE≌△DEC,
∴CE=AE,
在Rt△DEA中,AE=
=4,
∴CE=4.
(1)∵DE平分∠ADC,CA平分∠BCD,
∴∠ADC=2∠CDE=116°,∠BCD=2∠ACD=64°
∵∠ADC+∠BCD=116°+64°=180°
∴AD∥BC;
(2)∵∠DCC=180°-∠ACD-∠CDE=90°,
∴DF⊥AC,
在△DAE和△DEC中
|
∴△DAE≌△DEC,
∴CE=AE,
在Rt△DEA中,AE=
| AD2-DE2 |
∴CE=4.
看了 如图,四边形ABCD中,∠A...的网友还看了以下:
已知平面a交平面b=L,A平行于a,A平行于b,求证:A平行于L 2020-04-05 …
已知直线a平行于平面α,直线a平行于平面β,平面α∩平面β=b,求证a平行b 2020-04-05 …
直角三角形中,一条直角边为a一条直角边为b斜边为c,斜边上的高为h,求证a平方分之一加b平方分之一 2020-05-22 …
设向量a=(4cosA,sinA),b=(sinB,4cosB),c=(cosB,-4sinB)( 2020-06-18 …
已知A平方+B平方+C平方-10A-24B-26C+338=0,求证A平方+B平方=C平方 2020-07-17 …
已知A平方+B平方+C平方-10A-24B-26C+338=0求证A平方+B平方=C平方 2020-07-19 …
已知b分之a=d分之c,求证:点开看,打不下了-求证a平方分之一+b平方分之一+c平方分之一+d平 2020-07-25 …
勾股定理超难的题十级以上再进吧!将直角三角形ABC绕直角顶点C旋转,使点A落在BC边上的A',利用 2020-07-29 …
在学习中,我们经常看到这种现象:有的同学平时学习很好,但考试时却考不出好成绩,而有的同学平时学习不是 2020-12-13 …
6.“良好的情绪是保证水平正常发挥,甚至超水平发挥的重要因素。”这句话的意思是()A.平时训练是次要 2021-01-19 …