早教吧作业答案频道 -->数学-->
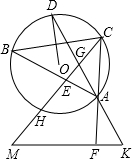
已知,如图,O是△ABC的外接圆,OD⊥BC交O于点D,CE平分∠ACB交AB于点E,交O于点H,AD与CH相交于点G,延长CH到点M,使MH=HG,延长DA到点K,使AK=AG,CA的延长线交MK于点F,求证:ME=MF.
题目详情
已知,如图, O是△ABC的外接圆,OD⊥BC交 O于点D,CE平分∠ACB交AB于点E,交 O于点H,AD与CH相交于点G,延长CH到点M,使MH=HG,延长DA到点K,使AK=AG,CA的延长线交MK于点F,求证:ME=MF.

▼优质解答
答案和解析
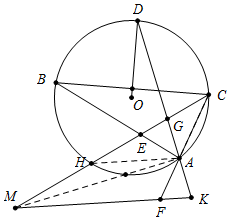
证明:如图,连接AH、AM.
∵OD⊥BC,
∴
=
,
∴∠BAD=∠CAD,
∵∠BCH=∠ACH,∠BCH=∠BAH,
∴∠BAH=∠ACH,
∵∠HGA=∠ACH+∠CAG,∠HAG=∠BAH+∠BAD,
∴∠HGA=∠HAG,
∴HA=GH=HM,
∴△MAG是直角三角形,
∴MA⊥KG,
∵AG=AK,
∴MG=MK,
∴∠AGE=∠K,
∵∠FAK=∠CAD,∠BAD=∠DAC,
∴∠EAG=∠FAK,
在△AGE和△AKF中,
,
∴△AGE≌△AKF,
∴EG=FK,∵MG=MK,
∴ME=MF.

∵OD⊥BC,
∴
 |
| DB |
 |
| DC |
∴∠BAD=∠CAD,
∵∠BCH=∠ACH,∠BCH=∠BAH,
∴∠BAH=∠ACH,
∵∠HGA=∠ACH+∠CAG,∠HAG=∠BAH+∠BAD,
∴∠HGA=∠HAG,
∴HA=GH=HM,
∴△MAG是直角三角形,
∴MA⊥KG,
∵AG=AK,
∴MG=MK,
∴∠AGE=∠K,
∵∠FAK=∠CAD,∠BAD=∠DAC,
∴∠EAG=∠FAK,
在△AGE和△AKF中,
|
∴△AGE≌△AKF,
∴EG=FK,∵MG=MK,
∴ME=MF.
看了 已知,如图,O是△ABC的外...的网友还看了以下:
在一个不导热的密闭反应中,只发生两个反应a(g)+b(g)=2c(g),焓变小于0x(g)+3y( 2020-04-26 …
1.f(x)=x+a/x(a属于R),g(x)=lnx若关于x的方程g(x)/X的平方=f(x)- 2020-04-27 …
已知:如图在平行四边形ABCD中,对角线AC、BD相交于点O,EF、GD过点O,EF分别交AB,C 2020-05-15 …
已知e为平行四边形abcd中dc边延长线上一点,且ce=dc,连ae分别交bc bd于f g,连已 2020-05-16 …
mA(g)+nB(g)可逆等于pC(g)+qD(g)①va:vb:vc:vd=m:n:p:q--- 2020-06-07 …
对于两个数p和q,即算术平均数A、几何平均数G、调和平均数H,其中A=p+q/2对于两个数和有三种 2020-06-12 …
来个人,化学平衡晕死了,我写的对不M(G)+N(G)=P(G)+Q(G)压强一定,不平衡M(G)+ 2020-07-04 …
为什么氨气在水中解离到平衡的ΔG=0? 2020-07-22 …
离散数学题,对于任意的简单平面图G,证明K(G)≦λ(G)≦δ(G)对于任意的简单平面图G,证明K 2020-08-01 …
在数学上,对于两个正数p和q有三种平均数,即算术平均数A、几何平均数G、调和平均数H,其中A=p+ 2020-08-03 …