早教吧作业答案频道 -->数学-->
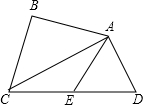
如图，在四边形ABCD中，∠ABC=90°，∠BAD=135°，AB=1，AC=2，点E为CD中点．求证：CD=2AE．
题目详情
如图，在四边形ABCD中，∠ABC=90°，∠BAD=135°，AB=1，AC=
，点E为CD中点．求证：CD=2AE．
| 2 |
▼优质解答
答案和解析
证明：Rt△ABC中，∠ABC=90°，
AB=1，AC=
∴BC2=（
）2-12=1，
∴BC=AB，
∴∠BCA=∠BAC=45°，
又∵∠BAD=135°，
∴∠CAD=135-45°=90°，
又∵AE为CD上中点，
∴AE为Rt△CAD斜边上中线，则CD=2AE．
AB=1，AC=
| 2 |
∴BC2=（
| 2 |
∴BC=AB，
∴∠BCA=∠BAC=45°，
又∵∠BAD=135°，
∴∠CAD=135-45°=90°，
又∵AE为CD上中点，
∴AE为Rt△CAD斜边上中线，则CD=2AE．
看了 如图，在四边形ABCD中，∠...的网友还看了以下：
求证:两椭圆b^2x^2+a^2y^2-a^2b^2=0,a^2x^2+b^2y^2-a^2b^2 2020-04-06 …
请在这里概述您的问题问一道数学题步骤,表示没看懂已知函数f(x)=x^2+a/x(x≠0,常数a∈ 2020-05-13 …
在三角形ABC中,a,b,c分别表示角A,B,C对应的三边,（1）若b^2+c^2-a^2=bc, 2020-07-13 …
已知|ab-2|+|a-1|=0，则：a=，b=．在此条件下，计算：1ab+1(a+1)(b+1) 2020-07-20 …
1.在三角形abc中,证明a/b-b/a=c(CosB/b-CosA/a)2.在三角形abc中,已 2020-07-21 …
证明：如果正整数a,b,c满足c^2=a^2+b^2,则必然存在正整数x,y使得c=x^2+y^2 2020-07-22 …
已知命题p:"对任意x属于[1,2],x^2-a>=0",命题q:"存在x0属于R,x0^2+2a 2020-07-29 …
1.已知方程x^2-（bcosA)x+acosB=0的两根之和等于两根之积,且a,b为△ABC的两 2020-08-02 …
基本不等式的使用问题a+b=1,求(a+2)^2+(b+2)^2的最小值.在这道题里,如果使用基本 2020-08-03 …
圆的特殊方程过原点:x^2+y^2+ax+by=0圆心在x轴上:(x-a)^2+y^2=r^2圆心在 2020-11-01 …