早教吧作业答案频道 -->物理-->
如图所示,在粗糙水平面上A点固定一半径R=0.2m的竖直光滑圆弧轨道,底端有一小孔,在水平面上距A点s=1m的B点正上方O处,用长为L=0.9m的轻绳悬挂一质量M=0.1kg的小球甲,现将小球甲拉至图中C
题目详情
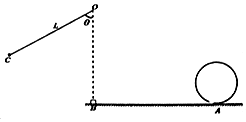
如图所示,在粗糙水平面上A点固定一半径R=0.2m的竖直光滑圆弧轨道,底端有一小孔,在水平面上距A点s=1m的B点正上方O处,用长为L=0.9m的轻绳悬挂一质量M=0.1kg的小球甲,现将小球甲拉至图中C位置,绳与竖直方向夹角θ=60°,静止释放小球甲,摆到最低点B点时与另一质量m=0.05kg的静止小滑块乙(可视为质点)发生完全弹性碰撞,碰后小滑块乙在水平面上运动到A点,并无碰撞地经过小孔进入圆弧轨道,当小滑块乙进入圆轨道后立即关闭小孔,g=10m/s2
(1)求甲、乙碰前瞬间小球甲的速度大小
(2)若小滑块乙进入圆轨道后的运动过程中恰好不脱离圆弧轨道,求小滑块乙与水平面的动摩擦因数μ

(1)求甲、乙碰前瞬间小球甲的速度大小
(2)若小滑块乙进入圆轨道后的运动过程中恰好不脱离圆弧轨道,求小滑块乙与水平面的动摩擦因数μ
▼优质解答
答案和解析
(1)甲球在下摆过程中,根据机械能守恒定律得
MgL(1-cos60°)=
M
可得 v0=
=
=3m/s
(2)设甲乙碰撞后速度分别为v1和v2.取向右为正方向,由动量守恒定律得
Mv0=Mv1+mv2.
根据动能守恒得:
M
=
Mv12+
mv22.
联立解得 v2=4m/s
小滑块乙进入圆轨道后的运动过程中恰好不脱离圆弧轨道,有两种情况:
第一种情况:乙刚好通过与圆心等高的位置,从B到圆心等高的位置,由动能定理有
-μmgs-mgR=0-
mv22.
解得 μ=0.6
第二种情况:乙恰好通过圆轨道的最高点,则有
mg=m
从B点到圆周最高点的过程,由动能定理得;
-μ′mgs-mg•2R=
mv2-
mv22.
解得 μ′=0.3
所以乙恰好不脱离圆弧轨道,小滑块乙与水平面的动摩擦因数μ是0.6或0.3.
答:
(1)甲、乙碰前瞬间小球甲的速度大小是3m/s.
(2)若小滑块乙进入圆轨道后的运动过程中恰好不脱离圆弧轨道,小滑块乙与水平面的动摩擦因数μ是0.6或0.3.
MgL(1-cos60°)=
| 1 |
| 2 |
| v | 2 0 |
可得 v0=
| gL |
| 0.9×10 |
(2)设甲乙碰撞后速度分别为v1和v2.取向右为正方向,由动量守恒定律得
Mv0=Mv1+mv2.
根据动能守恒得:
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| 1 |
| 2 |
联立解得 v2=4m/s
小滑块乙进入圆轨道后的运动过程中恰好不脱离圆弧轨道,有两种情况:
第一种情况:乙刚好通过与圆心等高的位置,从B到圆心等高的位置,由动能定理有
-μmgs-mgR=0-
| 1 |
| 2 |
解得 μ=0.6
第二种情况:乙恰好通过圆轨道的最高点,则有
mg=m
| v2 |
| R |
从B点到圆周最高点的过程,由动能定理得;
-μ′mgs-mg•2R=
| 1 |
| 2 |
| 1 |
| 2 |
解得 μ′=0.3
所以乙恰好不脱离圆弧轨道,小滑块乙与水平面的动摩擦因数μ是0.6或0.3.
答:
(1)甲、乙碰前瞬间小球甲的速度大小是3m/s.
(2)若小滑块乙进入圆轨道后的运动过程中恰好不脱离圆弧轨道,小滑块乙与水平面的动摩擦因数μ是0.6或0.3.
看了 如图所示,在粗糙水平面上A点...的网友还看了以下:
一个很简单的微分中值定理运用题已知函数f(x)在区间[0,1]上连续,在(0,1)内可导,且f(0) 2020-03-31 …
(32)以下哪个地址为回送地址? ( )A)128.o.0.1 B)127.0.0.1 C)126. 2020-05-23 …
理想函数问题对于定义域为[0,1]的函数f(x),如果同时满足一下三条:1.对任意的x∈[0,1] 2020-06-07 …
对于定义域为[0,1]的函数f(x),如果同时满足一下三条:1.对任意的x∈[0,1],总有f(x 2020-06-07 …
设u=u(x),v=v(x)都是可微函数,则d(uυ)=()A.udv+υdvB.u′dυ+u′d 2020-07-20 …
求一高数题证明设f(x)∈C(2)(-1,1),且f"(x)≠0,试证(1)对(-1,1)内任一点 2020-07-20 …
1.53米,他的实际高度应在几米之间?(关于准确数与近似数的)0.1^2=0.01,0.01^2= 2020-07-31 …
请分析一下四个选项intw[3][4]o={{0,1},{2,4},{5,8}};int(*p)[ 2020-08-03 …
对定义在[0,1]上,并且同时满足以下两个条件的函数f(x)称为G函数.①对任意的x∈[0,1], 2020-08-03 …
已知函数f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0,f(1)=1.证明:(已知函 2020-11-02 …