早教吧作业答案频道 -->数学-->
如图,已知正方形ABCD的对角线交于O点,点E、F分别是AO、CO的中点,连接BE、BF、DE、DF,则下列结论中一定成立的是(把所有正确结论的序号都填在横线上)①BF=DE;②∠ABO=2∠ABE;③S△AED=
题目详情
如图,已知正方形ABCD的对角线交于O点,点E、F分别是AO、CO的中点,连接BE、BF、DE、DF,则下列结论中一定成立的是___(把所有正确结论的序号都填在横线上)
①BF=DE;②∠ABO=2∠ABE;③S△AED=
S△ACD;④四边形BFDE是菱形.
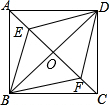
①BF=DE;②∠ABO=2∠ABE;③S△AED=
| 1 |
| 4 |

▼优质解答
答案和解析
∵点E、F分别是AO、CO的中点,
∴OE=OF,
∵四边形ABCD是正方形,
∴OD=OB,AC⊥BD,
∴四边形BEDF是平行四边形,
∴BF=DE,故选项①正确;
∵四边形BEDF是平行四边形,AC⊥BD,
∴四边形BFDE是菱形,故选项④正确;
∵△AED的一边AE是△ACD的边AC的
,且此边的高相等,
∴S△ABD=
S△ACD;故选项③正确,
∵AB>BO,BE不垂直于AO,
∴BE不是∠ABO的角平分线,
∴∠ABO≠2∠ABE;故选项②没有足够的条件证明成立,
故答案为:①③④.
∵点E、F分别是AO、CO的中点,
∴OE=OF,
∵四边形ABCD是正方形,
∴OD=OB,AC⊥BD,
∴四边形BEDF是平行四边形,
∴BF=DE,故选项①正确;

∵四边形BEDF是平行四边形,AC⊥BD,
∴四边形BFDE是菱形,故选项④正确;
∵△AED的一边AE是△ACD的边AC的
| 1 |
| 4 |
∴S△ABD=
| 1 |
| 4 |
∵AB>BO,BE不垂直于AO,
∴BE不是∠ABO的角平分线,
∴∠ABO≠2∠ABE;故选项②没有足够的条件证明成立,
故答案为:①③④.
看了 如图,已知正方形ABCD的对...的网友还看了以下:
如图,在△ABC中,以AB为直径作⊙O交BC于点D,DE交AC于E.(1)若AB=AC,DE⊥AC 2020-05-16 …
如图所示,△ABC是直角三角形,∠ABC=90°,以AB为直径的⊙O交AC于点E,点D是BC边的中 2020-05-17 …
如图,在△ABC中,∠BAC=90°,AB=AC,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC于 2020-06-12 …
如图O是△ABC中∠A、∠B、∠C平分线的交点,DE过O且DE⊥AO于O点,D、E分别在AB、AC 2020-07-22 …
如图,AB为⊙O的直径,AD平分∠BAC交⊙O于点D,DE⊥AC交AC的延长线于点E,BF⊥AB交 2020-07-29 …
如图,在△ABC中,∠BAC=90°,AB=AC,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC于点 2020-11-03 …
如图1,BC是O的直径,点A在O上,点D在CA的延长线上,DE⊥BC,垂足为点E,DE与O相交于点H 2020-11-03 …
如图,AB为⊙O的直径,C为圆上一点,AD平分∠BAC交⊙O于点D,DE⊥AC交AC的延长线于点E, 2020-12-01 …
如图,已知AB、AC分别是⊙O的直径和弦,D为BC的中点,DE垂直于AC的延长线于点E,连结BC,若 2021-01-02 …
如图,AB为⊙O的直径,AD平分∠BAC交⊙O于点D,DE⊥AC交AC的延长线于点E,BF⊥AB交A 2021-01-02 …