早教吧作业答案频道 -->数学-->
如图,直线l与O相离,过点O作OA⊥l,垂足为A,OA交O于点B,点C在直线l上,连接CB并延长交O于点D,在直线l上另取一点P,使∠PCD=∠PDC.(1)求证:PD是O的切线;(2)若AC=1,AB=2,PD=6,求
题目详情
如图,直线l与 O相离,过点O作OA⊥l,垂足为A,OA交 O于点B,点C在直线l上,连接CB并延长交 O于点D,在直线l上另取一点P,使∠PCD=∠PDC.
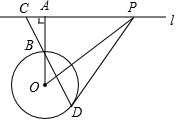
(1)求证:PD是 O的切线;
(2)若AC=1,AB=2,PD=6,求 O的半径r和△PCD的面积.

(1)求证:PD是 O的切线;
(2)若AC=1,AB=2,PD=6,求 O的半径r和△PCD的面积.
▼优质解答
答案和解析
(1)连接OD,
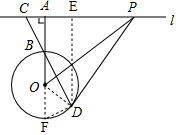
∴∠ABC=∠OBD=∠ODB,
∵OA⊥l,
∴∠PCD+∠ABC=90°,
∴∠PCD+∠ODB=90°,
∵∠PCD=∠PDC,
∴∠PDC+∠ODB=90°,即∠ODP=90°,
∴PD是 O的切线;
(2)∵∠PCD=∠PDC,
∴PC=PD=6,
∴PA=5,
设OB=OF=OD=r,
由PA2+AO2=PD2+OD2可得52+(2+r)2=62+r2,
解得:r=
,
延长AO交 O于点F,连接DF,
∵∠ABC=∠DBF、∠BAC=∠BDF=90°,
∴△ABC∽△DBF,
∴
=
,即
=
,
∴DB=
,
过点D作DE⊥PC于点E,
∴△CAB∽△CED,
∴
=
,即
=
,
解得:DE=
,
∴S△PCD=
PC•DE=
×6×
=
.

∴∠ABC=∠OBD=∠ODB,
∵OA⊥l,
∴∠PCD+∠ABC=90°,
∴∠PCD+∠ODB=90°,
∵∠PCD=∠PDC,
∴∠PDC+∠ODB=90°,即∠ODP=90°,
∴PD是 O的切线;
(2)∵∠PCD=∠PDC,
∴PC=PD=6,
∴PA=5,
设OB=OF=OD=r,
由PA2+AO2=PD2+OD2可得52+(2+r)2=62+r2,
解得:r=
| 7 |
| 4 |
延长AO交 O于点F,连接DF,
∵∠ABC=∠DBF、∠BAC=∠BDF=90°,
∴△ABC∽△DBF,
∴
| AB |
| DB |
| BC |
| BF |
| 2 |
| DB |
| ||
|
∴DB=
7
| ||
| 5 |
过点D作DE⊥PC于点E,
∴△CAB∽△CED,
∴
| AB |
| ED |
| CB |
| CD |
| 2 |
| DE |
| ||||||
|
解得:DE=
| 24 |
| 5 |
∴S△PCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 24 |
| 5 |
| 72 |
| 5 |
看了 如图,直线l与O相离,过点O...的网友还看了以下:
己知PE、PF是O的切线,A、B是一组对径点,PB交O于另一点C,直线AF、BE交于D点.求证:∠ 2020-04-07 …
如图,AB是⊙O的切线,B为切点,BC是⊙O的弦,直线AC与⊙O交于D,角C=45°,DE⊥AB, 2020-07-11 …
如图,已知点A(0,2),直线l:y=-x-2与x轴交于D点,与y轴交于E点,B是直线l上的一个动 2020-07-26 …
如图,⊙O的直径AB=12cm,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别 2020-07-31 …
如图,△ABC是等边三角形,⊙O与AC相切于A点,与BC交于E点,与AB的延长线交于D点.已知BE 2020-07-31 …
如图,AB是圆O的直径,P为圆外一点,PB是圆O的切线,PA是圆O的割线且与圆O相交于点C.过点C 2020-07-31 …
1.MT与圆O相切于T,MAB是圆的一条割线,过C点作AC∥MT,连结MC与圆相交于D连结BD并延 2020-07-31 …
三角形内切圆难题三角形ABC的内切圆与AC.AB.BC.分别交于D.E.F.已知AC等于7.AB等 2020-08-01 …
(2001•贵阳)已知:如图,⊙O2过⊙O1的圆心O1,且与⊙O1内切于点P,弦AB切⊙O2于点C, 2020-11-13 …
如图,PA与O切于点A,过点P的割线与弦AC交于B,与O交于D、E,且PA=PB=BC,若PD=4, 2020-12-05 …