早教吧作业答案频道 -->数学-->
如图,⊙O的直径AB=12cm,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于D,C两点.(Ⅰ)若∠ADC=122°,求∠BCD的度数;(Ⅱ)设AD=x,BC=y,求y关于x的函数解析式.
题目详情
如图,⊙O的直径AB=12cm,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于D,C两点.
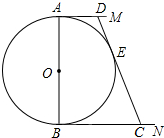
(Ⅰ)若∠ADC=122°,求∠BCD的度数;
(Ⅱ)设AD=x,BC=y,求y关于x的函数解析式.

(Ⅰ)若∠ADC=122°,求∠BCD的度数;
(Ⅱ)设AD=x,BC=y,求y关于x的函数解析式.
▼优质解答
答案和解析
(I)∵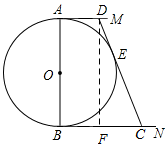 AD与BC都是⊙O的切线,
AD与BC都是⊙O的切线,
∴∠OAD=∠OBC=90°,
∴∠OAD+∠OBC=180°,
∴AD∥BC,
∴∠BCD+∠ADC=180°,
∴∠BCD=58°;
(II)过点D作DF⊥BC于点F,可知AB=CD=12,
∵AM和BN是⊙O的两条切线,DE与⊙O相切于点E,
∴AD=DE=x,BC=CE=y,
∴CD=DE+CE=x+y,
∴CF=BC-BF=y-x,
在Rt△DFC中,
∴由勾股定理可知:DF2+FC2=CD2,
122+(y-x)2=(x+y)2
∴化简可得:y=
 AD与BC都是⊙O的切线,
AD与BC都是⊙O的切线,∴∠OAD=∠OBC=90°,
∴∠OAD+∠OBC=180°,
∴AD∥BC,
∴∠BCD+∠ADC=180°,
∴∠BCD=58°;
(II)过点D作DF⊥BC于点F,可知AB=CD=12,
∵AM和BN是⊙O的两条切线,DE与⊙O相切于点E,
∴AD=DE=x,BC=CE=y,
∴CD=DE+CE=x+y,
∴CF=BC-BF=y-x,
在Rt△DFC中,
∴由勾股定理可知:DF2+FC2=CD2,
122+(y-x)2=(x+y)2
∴化简可得:y=
| 36 |
| x |
看了 如图,⊙O的直径AB=12c...的网友还看了以下:
如图,一群速率不同的一价离子从A.B两平行极板正中央水平射入偏转电场,A.B间电压为U,间距为d. 2020-07-06 …
用A、B、C三种塑料板如图(每种都由若干个1×1的正方形组成),拼成10个5×5的正方形.已有A型 2020-07-07 …
下列各句中,标点符号使用正确的一句是()A.他一个人在教室里想着、写着,几乎忘记了一切.B.“到底 2020-07-15 …
如图,在矩形ABCD中,AB=3,AD=10,P是AD边上动点(不与A,D重合),⊙B是以B为圆心 2020-07-24 …
下列句子中,加点成语使用不恰当的一句是()A.人要是有一颗象草木一样“不怨寒暑移”的心,就不会抱怨 2020-07-24 …
如图,已知圆心为A,B,C的三个圆彼此相切,且均与直线l相切.若⊙A,⊙B,⊙C的半径分别为a,b 2020-07-31 …
过点作圆的两条切线,切点分别为A,B,已知,若,则的最小值是A.B.C.D. 2020-07-31 …
若在曲线上两个不同点处的切线重合,则称这条切线为曲线的“自公切线”.下列方程:①;②;③;④对应的 2020-08-01 …
下列对本诗的理解不正确的一项是()A.首句“清晨入古寺”点明了出游的时间和地点.诗人一大早就“入古寺 2020-11-28 …
下列加点成语使用正确的一项是()A.在与洪涝灾害的斗争中,全体指战员不畏艰险,奋力拼搏,终于取得最后 2020-12-12 …