早教吧作业答案频道 -->数学-->
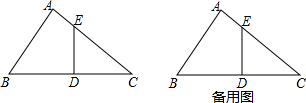
如图1,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.(1)求ED、EC的长;(2)若BP=2,求CQ的长.
题目详情
如图1,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.
(1)求ED、EC的长;
(2)若BP=2,求CQ的长.
(1)求ED、EC的长;
(2)若BP=2,求CQ的长.

▼优质解答
答案和解析
:(1)如图1,∵∠A=90°,AB=6,AC=8,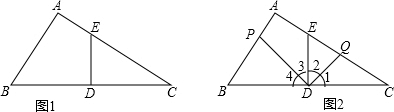
∴根据勾股定理得到,BC=
=10
∴CD=
BC=5.
∵DE⊥BC.
∴∠A=∠CDE=90°∠C=∠C
∴△CDE∽△CAB
∴DE:AB=CE:CB=CD:CA,
即DE:6=CE:10=5:8
∴DE=
,CE=
;
(2)如图2,∵△CDE∽△CAB,
∴∠B=∠DEC.
∵∠PDQ=90°
∴∠1+∠4=90°.
∵∠1+∠2=90°
∴∠2=∠4,
∴△PBD∽△QED,
∴
=
,
∴
=
,
∴EQ=
,
∴CQ=CE-EQ=
-
=
.
如图2-1,∵∠B=DEC,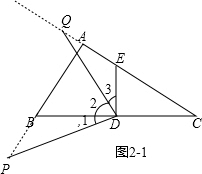
∴∠PBD=∠QED.
∵∠PDQ=90°
∴∠1+∠2=90°.
∵∠3+∠2=90°
∴∠1=∠3,
∴△PBD∽△QED
∴
=
,
∴
=
,
∴EQ=
,
∴CQ=
+
=
,
故CQ=
或
;

∴根据勾股定理得到,BC=
| AB2+AC2 |
∴CD=
| 1 |
| 2 |
∵DE⊥BC.
∴∠A=∠CDE=90°∠C=∠C
∴△CDE∽△CAB
∴DE:AB=CE:CB=CD:CA,
即DE:6=CE:10=5:8
∴DE=
| 15 |
| 4 |
| 25 |
| 4 |
(2)如图2,∵△CDE∽△CAB,
∴∠B=∠DEC.
∵∠PDQ=90°
∴∠1+∠4=90°.
∵∠1+∠2=90°
∴∠2=∠4,
∴△PBD∽△QED,
∴
| PB |
| EQ |
| BD |
| ED |
∴
| 2 |
| EQ |
| 5 | ||
|
∴EQ=
| 3 |
| 2 |
∴CQ=CE-EQ=
| 25 |
| 4 |
| 3 |
| 2 |
| 19 |
| 4 |
如图2-1,∵∠B=DEC,

∴∠PBD=∠QED.
∵∠PDQ=90°
∴∠1+∠2=90°.
∵∠3+∠2=90°
∴∠1=∠3,
∴△PBD∽△QED
∴
| PB |
| EQ |
| BD |
| ED |
∴
| 2 |
| QE |
| 5 | ||
|
∴EQ=
| 3 |
| 2 |
∴CQ=
| 25 |
| 4 |
| 3 |
| 2 |
| 31 |
| 4 |
故CQ=
| 19 |
| 4 |
| 31 |
| 4 |
看了 如图1,在Rt△ABC中,∠...的网友还看了以下:
设抛物线C1的方程为y=120x2,它的焦点F关于原点的对称点为E.若曲线C2上的点到E、F的距离 2020-04-26 …
已知点E,F为长方形ABCD的边上的点,且E(1,0),F(4,3),有知长方形的长为6,宽为4, 2020-05-17 …
(1)打点计时器电源频率为50Hz.图1中A、B、C、D、E、F、G是纸带上7个连续的点,E点读数 2020-06-16 …
如图所示,已知四边形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在 2020-06-17 …
如图,点E,F分别是菱形ABCD中BC,CD边上的点(E,F不与B,C,D重合)在添辅助线的情况下 2020-07-15 …
数轴上表示-2分之1的点在表示-1点边;数轴上表示+2分之1的点在表示+1的点边. 2020-07-30 …
证明:若直线上的点集E的任意两点之间的距离大于1,则集合E是有限的或者可数的.我对这道题有思路,但 2020-07-30 …
如图所示,△ABC的三个顶点在O上,D是AB上的点,E是AC上的点,若∠BAC=50°.则∠D+∠ 2020-07-30 …
数学题目已知P为平行四边形ABCD内一点,过点P分别作AB,AD的平行线交平行四边形的四边E,F, 2020-08-01 …
如图,点E、F分别是菱形ABCD中BC、CD边上的点(E、F不与B、C、D重合);在不作任何辅助线 2020-08-01 …