早教吧作业答案频道 -->数学-->
已知函数f（x）=|x2+5x+4|，x≤02|x-2|，x>0，若函数y=f（x）-a|x|恰有4个零点，则实数a的取值
题目详情
已知函数f（x）=
，若函数y=f（x）-a|x|恰有4个零点，则实数a的取值范围为___．
| |
|
▼优质解答
答案和解析
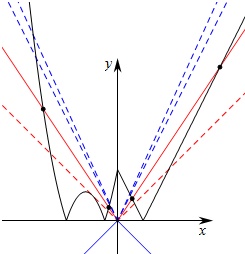由y=f（x）-a|x|=0得f（x）=a|x|，
作出函数y=f（x），y=a|x|的图象，
当a≤0，不满足条件，
∴a>0，
当a≥2时，此时y=a|x|与f（x）有三个 交点，
当a=1时，
当x<0时，f（x）=-x2-5x-4，
由f（x）=-x2-5x-4=-x
得x2+4x+4=0，
则判别式△=16-4×4=0，
即此时直线y=-x与f（x）相切，
此时y=a|x|与f（x）有五个交点，
∴要使函数y=f（x）-a|x|恰有4个零点，
则1故答案为：（1，2）
由y=f（x）-a|x|=0得f（x）=a|x|，作出函数y=f（x），y=a|x|的图象，
当a≤0，不满足条件，
∴a>0，
当a≥2时，此时y=a|x|与f（x）有三个 交点，
当a=1时，
当x<0时，f（x）=-x2-5x-4，
由f（x）=-x2-5x-4=-x
得x2+4x+4=0，
则判别式△=16-4×4=0，
即此时直线y=-x与f（x）相切，
此时y=a|x|与f（x）有五个交点，
∴要使函数y=f（x）-a|x|恰有4个零点，
则1
看了 已知函数f（x）=|x2+5...的网友还看了以下：
一道有关函数单调性的问题求证题：函数f(x)=x+x分之a(a>0）在区间（0.根号a)上是减函数我 2020-03-30 …
已知函数f(x)=x^2+x-ln(x+a)+3b在x=0出取得极值0.(1)求实数a,b的值(这个 2020-03-30 …
已知函数f(x)=ax^3+bx²,曲线y=f(x)过点P(-1,2),且在点P处的切线恰好与直线 2020-05-21 …
已知函数f(x)=x²+3x|x-a|，其中a∈R，（1）当a＞0时，方程f（x）=3恰有三个根， 2020-06-27 …
设函数f(x)＝，g(x)＝f(x)－b．若存在实数b，使得函数g(x)恰有3个零点，则实数a的取 2020-06-27 …
已知以T=4为周期的函数f(x)=已知以T=4为周期的函数f(x)=m*根号下(1-x^2),x∈ 2020-08-02 …
已知函数f(x)=1/3*x^3+[(1-a)/2]*x^2-ax-a,x∈R其中a>0.若函数f( 2020-11-10 …
已知函数f(x)=e^x-ax-1,a＞0(1)若函数f(x)恰有一个零点,证明：a^a=e^(a- 2020-12-26 …
已知函数f(x)=x-lnx.求函数f(x)的极值?若关于x的方程f(x)+2x=x^2+b在[1/ 2020-12-31 …
已知函数f（x）是定义在R上的偶函数，已知x≥0时，f（x）=x2-2x．（1）画出偶函数f（x）的 2021-01-15 …