早教吧作业答案频道 -->数学-->
如图,∠MAN=60°,点B在射线AM上,AB=4,点P为直线AN上一动点,以BP为边作等边三角形BPQ(点B,P,Q按顺时针排列),点O是△BPQ的外心.(1)如图1,当OB⊥AM时,点O∠MAN的平分线上(填“
题目详情
如图,∠MAN=60°,点B在射线AM上,AB=4,点P为直线AN上一动点,以BP为边作等边三角形BPQ(点B,P,Q按顺时针排列),点O是△BPQ的外心.
(1)如图1,当OB⊥AM时,点O___∠MAN的平分线上(填“在”或“不在”);
(2)求证:当点P在射线AN上运动时,总有点O在∠MAN的平分线;
(3)当点P在射线AN上运动(点P与点A不重合)时,AO与BP交于点C,设AP=m,用m表示AC•AO;
(4)若点D在射线AN上,AD=2,圆I为△ABD的内切圆.当△BPQ的边BP或BQ与圆I相切时,请直接写出点A与点O的距离.
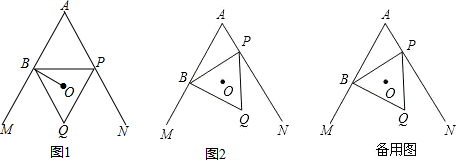
(1)如图1,当OB⊥AM时,点O___∠MAN的平分线上(填“在”或“不在”);
(2)求证:当点P在射线AN上运动时,总有点O在∠MAN的平分线;
(3)当点P在射线AN上运动(点P与点A不重合)时,AO与BP交于点C,设AP=m,用m表示AC•AO;
(4)若点D在射线AN上,AD=2,圆I为△ABD的内切圆.当△BPQ的边BP或BQ与圆I相切时,请直接写出点A与点O的距离.

▼优质解答
答案和解析
(1)在.
理由:如图1所示:连接OP.
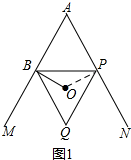
∵点O为等边△BQP的外心,
∴∠BOP=2∠BQP=120°,OB=OP.
∵OB⊥AM,
∴∠ABO=90°.
∵∠A+∠ABO+∠BOP+∠OPA=180°,
∴∠OPA=90°.
∴OP⊥AN.
∵OP=OB,OP⊥AN,OB⊥AM,
∴点O在∠MAN的平分线上.
(2)当点A与点P不重合时,如图2所示:连接OB、OP、OA.
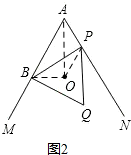
∵点O是等边三角形BOQ的外心,
∴∠BOP=120°,OP=OB.
∵∠BAP=60°,
∴∠BAP+∠BOP=180°.
∴点A、B、O、P共圆.
又∵OB=OP,
∴∠BAO=∠PAO.
∴点O在MAN的角平分线上.
当点P与点A重合时.
∵点O是等边三角形BOQ的外心,
∴PO平分∠BPQ.
∵∠BPQ与∠MAN重合,
∴∠PO平分∠MAN.
综上所示,总有点O在∠MAN的平分线.
(3)如图3所示:连接OB、OP、AO.
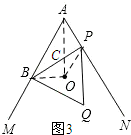
∵由(2)可知点B、O、P、A共圆,
∴∠BOA=∠BPA.
∵AO平分∠MAN,
∴∠BAO=∠PAO.
∴△ABO∽△ACP.
∴
=
.
∴AC•AO=AB•PA.
∴AC•AO=4m.
(4)如图4所示:当点P与点D重合时.
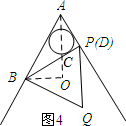
∵∠BAP=60°,BA=4,AD=2,
∴BP⊥AP.
∴∠BPA=90°.
又∵∠PAC=
∠MAN=30°,
∴∠OCB=∠ACP=60°.
∵O为等边三角形的外心,
∴∠OBC=30°.
∴∠BOC=90°.
在Rt△AOB中,OA=
AB=2
.
如图5所示:当点A与点P重合时.
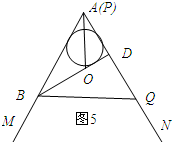
∵∠BAD=60°,BA=4,AD=2,
∴BD⊥AQ.
∴∠BDA=90°.
∵在Rt△AOD中,∠DAO=30°,AD=2,
∴AO=AD÷
=2×
=
.
如图6所示:
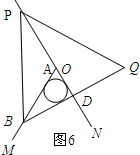
∵∠BAD=60°,BA=4,AD=2,
∴BD⊥AN.
∴∠BDA=90°.
∴∠ABD=30°
∵O为△BPQ的外心,
∴∠OBD=30°.
∴点A与点O重合.
∴OA=0.
综上所述,OA=2
或OA=
理由:如图1所示:连接OP.

∵点O为等边△BQP的外心,
∴∠BOP=2∠BQP=120°,OB=OP.
∵OB⊥AM,
∴∠ABO=90°.
∵∠A+∠ABO+∠BOP+∠OPA=180°,
∴∠OPA=90°.
∴OP⊥AN.
∵OP=OB,OP⊥AN,OB⊥AM,
∴点O在∠MAN的平分线上.
(2)当点A与点P不重合时,如图2所示:连接OB、OP、OA.

∵点O是等边三角形BOQ的外心,
∴∠BOP=120°,OP=OB.
∵∠BAP=60°,
∴∠BAP+∠BOP=180°.
∴点A、B、O、P共圆.
又∵OB=OP,
∴∠BAO=∠PAO.
∴点O在MAN的角平分线上.
当点P与点A重合时.
∵点O是等边三角形BOQ的外心,
∴PO平分∠BPQ.
∵∠BPQ与∠MAN重合,
∴∠PO平分∠MAN.
综上所示,总有点O在∠MAN的平分线.
(3)如图3所示:连接OB、OP、AO.

∵由(2)可知点B、O、P、A共圆,
∴∠BOA=∠BPA.
∵AO平分∠MAN,
∴∠BAO=∠PAO.
∴△ABO∽△ACP.
∴
| AB |
| AC |
| AO |
| AP |
∴AC•AO=AB•PA.
∴AC•AO=4m.
(4)如图4所示:当点P与点D重合时.

∵∠BAP=60°,BA=4,AD=2,
∴BP⊥AP.
∴∠BPA=90°.
又∵∠PAC=
| 1 |
| 2 |
∴∠OCB=∠ACP=60°.
∵O为等边三角形的外心,
∴∠OBC=30°.
∴∠BOC=90°.
在Rt△AOB中,OA=
| ||
| 2 |
| 3 |
如图5所示:当点A与点P重合时.

∵∠BAD=60°,BA=4,AD=2,
∴BD⊥AQ.
∴∠BDA=90°.
∵在Rt△AOD中,∠DAO=30°,AD=2,
∴AO=AD÷
| ||
| 2 |
2
| ||
| 3 |
4
| ||
| 3 |
如图6所示:

∵∠BAD=60°,BA=4,AD=2,
∴BD⊥AN.
∴∠BDA=90°.
∴∠ABD=30°
∵O为△BPQ的外心,
∴∠OBD=30°.
∴点A与点O重合.
∴OA=0.
综上所述,OA=2
| 3 |
4
|
看了 如图,∠MAN=60°,点B...的网友还看了以下:
数轴上两点A、B对应的数是-10,30啊点P从A点出发,沿数轴正方向以1单位长度/秒的速度匀速平移 2020-05-16 …
如图,△ABC在第一象限,其面积为8.点P从点A出发,沿△ABC的边从A-B-C-A运动一周,在点 2020-06-14 …
数学位置与坐标已知点p(2-m,3m+6),且点p到俩坐标轴的距离相等,求点p的坐标已知点p(m- 2020-06-30 …
如图,点P,Q分别在∠AOB的两边OA,OB上,若点N到∠AOB的两边距离相等,且PN=NQ,则点 2020-07-20 …
如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数y=4x(x>0)图象上位于直线下方的 2020-07-26 …
如图,点P是函数y=4/x在第一象限的图像上的任意一点,点P关于原点的对称点是P’,过点P做PA平 2020-07-29 …
在Rt△ABC中,∠ACB=90°,BC=30,AB=50,点P是AB边上任意一点,直线PE⊥AB, 2020-11-01 …
(2013•安庆三模)如图,倾斜角为θ的直线OP与单位圆在第一象限的部分交于点P,单位圆与坐标轴交于 2020-11-12 …
数轴上有ab两点,对应的数分别为-10,14,动点p,q分别从a,b,两点出发,且只有在数轴上运动, 2020-11-20 …
已知点M(-1,0),N(1,0),动点P(x,y)满足|PM|+|PN|=23,(1)求P的轨迹C 2020-11-27 …
 扫描下载二维码
扫描下载二维码