早教吧作业答案频道 -->数学-->
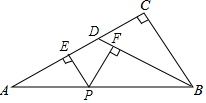
如图,在△ABC中,∠C=90°,AB=30,D是AB上一点,AD:CD=25:7,且DB=DA,过AB上一点P,作PE⊥AC于E,PF⊥BD于F,则PE+PF长是.
题目详情
如图,在△ABC中,∠C=90°,AB=30,D是AB上一点,AD:CD=25:7,且DB=DA,过AB上一点P,作PE⊥AC于E,PF⊥BD于F,则PE+PF长是___.

▼优质解答
答案和解析
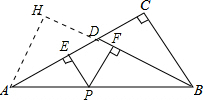 如图作AH⊥BD交BD的延长线于H,设AD=BD=25k,CD=7k,
如图作AH⊥BD交BD的延长线于H,设AD=BD=25k,CD=7k,
在Rt△DCB中,BC=
=24k,
在Rt△ACB中,∵AC2+BC2=AB2,
∴(32k)2+(24k)2=302,
∴k=
,
∴BC=18,
在△ADH和△BDC中,
,
∴△ADH≌△BDC,
∴AH=BC=18,
∵S△ABD=
•BD•AH=
•AD•PF+
•BD•PF,
∴PE+PF=AH=18,
故答案为18.
 如图作AH⊥BD交BD的延长线于H,设AD=BD=25k,CD=7k,
如图作AH⊥BD交BD的延长线于H,设AD=BD=25k,CD=7k,在Rt△DCB中,BC=
| BD2-CD2 |
在Rt△ACB中,∵AC2+BC2=AB2,
∴(32k)2+(24k)2=302,
∴k=
| 3 |
| 4 |
∴BC=18,
在△ADH和△BDC中,
|
∴△ADH≌△BDC,
∴AH=BC=18,
∵S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴PE+PF=AH=18,
故答案为18.
看了 如图,在△ABC中,∠C=9...的网友还看了以下:
为什么f(1-m)+f(1-m2)>0,即为f(1-m)>f(m2-1).求详解为什么f(1-m)+ 2020-03-30 …
设f(x)在[a,b]上l连续可导,且f(a)=f(b)=0,求证:存在η∈(a,b),使ηf(η 2020-05-14 …
设函数f(x),g(x)在[a,b]上连续,在(a,b)内可导,且f(a)=f(b)=0,证明存在 2020-05-14 …
求解一道高数题设f(x)在[a,b]上连续,(a,b)内可导,且f(a)=f(b)=0,证明:至少 2020-05-14 …
f(x在[a,b]上连续,f(a)=f(b)=0,且f’+(a)<0,为什么有在a的右邻域,f(x 2020-05-15 …
设函数f(x)=x^2-6x+5,集合A={(a,b)|f(a)+f(b)≤0,且f(a)-f(b 2020-06-03 …
高数题目设f(x)在[a,b]上可导,又f'(x)+[f(x)]^2-∫(a到x)f(t)dt=0 2020-06-12 …
一道高等数学题设f(x)在[a,b]上具有二阶导数,且f'(a)=f'(b)=0.试证在(a,b) 2020-06-16 …
设f(x)在(a,b)内存在一阶导数,若f(b)=0,且f'(x)>0,则f(x) 2020-06-18 …
设函数f(x)在[a,b]上连续,在(a,b)内可导,且f(a)=f(b)=0,试证在(a,b)内 2020-06-22 …