早教吧作业答案频道 -->数学-->
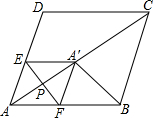
如图,在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF⊥AC分别交AD、AB于点E、F,将△AEF沿EF折叠,点A落在点A′处,当△A′BC是等腰三角形时,AP的长为.
题目详情
如图,在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF⊥AC分别交AD、AB于点E、F,将△AEF沿EF折叠,点A落在点A′处,当△A′BC是等腰三角形时,AP的长为___.

▼优质解答
答案和解析
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=5,∠DAC=∠BAC,
∵EF⊥AA′,
∴∠EPA=∠FPA=90°,
∴∠EAP+∠AEP=90°,∠FAP+∠AFP=90°,
∴∠AEP=∠AFP,
∴AE=AF,
∵△A′EF是由△AEF翻折,
∴AE=EA′,AF=FA′,
∴AE=EA′=A′F=FA,
∴四边形AEA′F是菱形,
∴AP=PA′
①当CB=CA′时,∵AA′=AC-CA′=3,∴AP=
AA′=
.
②当A′C=A′B时,∵∠A′CB=∠A′BC=∠BAC,
∴△A′CB∽△BAC,
∴
=
,
∴A′C=
,
∴AA=8-
=
,
∴AP=
AA′=
.
故答案为
或
.
∴AB=BC=CD=AD=5,∠DAC=∠BAC,
∵EF⊥AA′,
∴∠EPA=∠FPA=90°,

∴∠EAP+∠AEP=90°,∠FAP+∠AFP=90°,
∴∠AEP=∠AFP,
∴AE=AF,
∵△A′EF是由△AEF翻折,
∴AE=EA′,AF=FA′,
∴AE=EA′=A′F=FA,
∴四边形AEA′F是菱形,
∴AP=PA′
①当CB=CA′时,∵AA′=AC-CA′=3,∴AP=
| 1 |
| 2 |
| 3 |
| 2 |
②当A′C=A′B时,∵∠A′CB=∠A′BC=∠BAC,
∴△A′CB∽△BAC,
∴
| A′C |
| AB |
| BC |
| AC |
∴A′C=
| 25 |
| 8 |
∴AA=8-
| 25 |
| 8 |
| 39 |
| 8 |
∴AP=
| 1 |
| 2 |
| 39 |
| 16 |
故答案为
| 3 |
| 2 |
| 39 |
| 16 |
看了 如图,在菱形ABCD中,AB...的网友还看了以下:
圆锥曲线的已知椭圆C:x^2/2+y^2=1的右焦点为F,右准线为l,点A属于l,线段AF交C于点 2020-04-08 …
(1)已知函数f(x)=ax^2+c,且f'(1)=2,则a值为?(2)曲线y=e^(1)已知函数 2020-05-14 …
下图中a,b,c线为等压线,箭头表示A地风向,d,e线为等温线,g、f、h线为等高线。读图回答1~ 2020-05-15 …
图中a,b,c线为等压线,箭头表示A地风向,d、e线为等温线,g、f、h线为等高线,读图回答下列小 2020-05-15 …
如图,两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是菱形吗?求证:(1)四边形ABCD是平行四 2020-05-16 …
在矩形ABCD中,AD=5,AB=4,点E,F在直线AD上,且四边形BCFE为菱形.若线段EF的中 2020-07-09 …
.设f(x)在x.处可导,则lim△x→0△x分之f(x.-△x)-f(x.)等于?2.曲线y=3 2020-07-16 …
两道初二图形问题1.菱形的周长为16CM,一条对角线长为4倍根号3cm,则菱形的各个内角的大小分别 2020-07-30 …
在菱形ABCD中,∠B=60°,点E在射线BC上运动,∠EAF=60°,点F在射线CD上.(1)当 2020-07-30 …
已知在菱形ABCD中,∠ABC=60°,对角线AC、BD相交于点O,点E是线段BD上一动点(不与点B 2020-12-25 …