早教吧作业答案频道 -->数学-->
已知在菱形ABCD中,∠ABC=60°,对角线AC、BD相交于点O,点E是线段BD上一动点(不与点B,D重合),连接AE,以AE为边在AE的右侧作菱形AEFG,且∠AEF=60°.(1)如图1,若点F落在线段BD上,请
题目详情
已知在菱形ABCD中,∠ABC=60°,对角线AC、BD相交于点O,点E是线段BD上一动点(不与点B,D重合),连接AE,以AE为边在AE的右侧作菱形AEFG,且∠AEF=60°.
(1)如图1,若点F落在线段BD上,请判断:线段EF与线段DF的数量关系是___
(2)如图2,若点F不在线段BD上,其它条件不变,(1)中的结论是否仍然成立?请给出判断并予以证明;
(3)若点C,E,G三点在同一直线上,其它条件不变,请直接写出线段BE与线段BD的数量关系.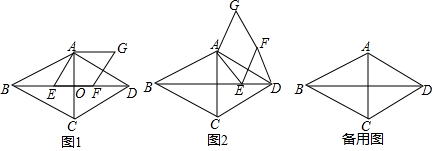
(1)如图1,若点F落在线段BD上,请判断:线段EF与线段DF的数量关系是___
(2)如图2,若点F不在线段BD上,其它条件不变,(1)中的结论是否仍然成立?请给出判断并予以证明;
(3)若点C,E,G三点在同一直线上,其它条件不变,请直接写出线段BE与线段BD的数量关系.

▼优质解答
答案和解析
(1)如图1,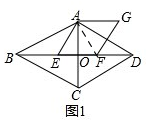 连接AF,
连接AF,
∵四边形ABCD是菱形,
∴AC⊥BD,∠ABO=
∠ABC=30°,
∴∠OAE=∠OAF=30°,
∴∠DAF=30°=∠ADO,
∴AF=FD,
∵AF=EF,
∴EF=FD;
∵∠AEF=60°,
∴∠BAE=30°=∠ABO,
∴AE=BE,
(2)成立,如图3,
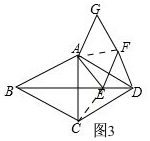 连接CE,AF,
连接CE,AF,
∵四边形ABCD是菱形,四边形AEFG是菱形,
∴AD=CD,AE=EF,BD垂直平分AC,∠ABC=∠ADC=60°,
∴∠ADC=∠AEF=60°,
∴△ACD和△AEF是等边三角形,
∴AC=AD,AE=AF=EF,∠CAD=∠EAF=60°,
∴∠CAE=∠DAF,
在△ACE和△ADF中,
,
△ACE≌△ADF,
∴EC=DF,
∵BD垂直平分AC,
∴EC=AE,
∴DF=AE=EF
(3)如图2,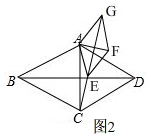 ∵AE=CE,
∵AE=CE,
∴∠ACE=∠CAE,
∵点C,E,G在同一条直线上,
∴∠AEG=2∠CAE=30°,
∴∠CAE=15°,
∵∠BAO=60°°,
∴∠BAE=75°,
∵∠ABO=
∠ABC=30°,
∴∠AEB=75°=∠BAE,
∴BE=AB,
在Rt△AOB中,∠ABO=30°,
∴cos∠ABO=
=
,
∴OB=
AB=
BE,
∴BD=2OB=
BE.
 连接AF,
连接AF,∵四边形ABCD是菱形,
∴AC⊥BD,∠ABO=
| 1 |
| 2 |
∴∠OAE=∠OAF=30°,
∴∠DAF=30°=∠ADO,
∴AF=FD,
∵AF=EF,
∴EF=FD;
∵∠AEF=60°,
∴∠BAE=30°=∠ABO,
∴AE=BE,
(2)成立,如图3,
 连接CE,AF,
连接CE,AF,∵四边形ABCD是菱形,四边形AEFG是菱形,
∴AD=CD,AE=EF,BD垂直平分AC,∠ABC=∠ADC=60°,
∴∠ADC=∠AEF=60°,
∴△ACD和△AEF是等边三角形,
∴AC=AD,AE=AF=EF,∠CAD=∠EAF=60°,
∴∠CAE=∠DAF,
在△ACE和△ADF中,
|
△ACE≌△ADF,
∴EC=DF,
∵BD垂直平分AC,
∴EC=AE,
∴DF=AE=EF
(3)如图2,
 ∵AE=CE,
∵AE=CE,∴∠ACE=∠CAE,
∵点C,E,G在同一条直线上,
∴∠AEG=2∠CAE=30°,
∴∠CAE=15°,
∵∠BAO=60°°,
∴∠BAE=75°,
∵∠ABO=
| 1 |
| 2 |
∴∠AEB=75°=∠BAE,
∴BE=AB,
在Rt△AOB中,∠ABO=30°,
∴cos∠ABO=
| OB |
| AB |
| ||
| 2 |
∴OB=
| ||
| 2 |
| ||
| 2 |
∴BD=2OB=
| 3 |
看了已知在菱形ABCD中,∠ABC...的网友还看了以下:
如图所示,P是矩形ABCD下方的一点,将△PCD绕P点顺时针旋转60°后恰好D点与A点重合,得到△ 2020-04-09 …
如图,P是矩形ABCD下方一点,将△PCD绕P点顺时针旋转60°后恰好D点与A点重合,得到△PEA 2020-04-09 …
△ABC是一个运动场,测得AC=80米,BC=60米,AB=100米.若线段CD是一条小渠,且D在 2020-05-21 …
一条杠杆a点为轴,d点到a点为30厘米,c点到a点3厘米,如果在b点施加10公斤的力量,那么c点可 2020-05-23 …
关于平面直角坐标系如图,A点的坐标为(3,2),B点的坐标为(0,0),C点的坐标为(4,0).要 2020-06-04 …
如图,P是矩形ABCD下方一点,将△PCD绕P点顺时针旋转60°后恰好D点与A点重合,得到△PEA 2020-06-13 …
如图,P是矩形ABCD下方一点,将△PCD绕P点顺时针旋转60°后恰好D点与A点重合,得到△PEA 2020-06-30 …
实验中学把一块三角形的废地开辟为植物园,如图所示,测得AC=80米,BC=60米,AB=100米. 2020-07-08 …
图中各点方位描述正确的是()A.A点在B点的东南方向B.D点在A点的正南方向C.C点在A点的东南方 2020-07-31 …
如图,D为等边三角形ABC的边BC上一点...D为等边△ABC的边BC上一点,且点E在线段AD上( 2020-08-03 …