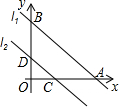
如图，已知直线l1：y=-34x+6与x轴交于点A，与y轴交于点B，将直线l1向下平移4个单位长度后得到直线l2，直线l2与x轴交于点C，与y轴交于点D．（1）求△AOB的面积；（2）直线l

Question

如图，已知直线l₁：y=- (3)/(4)x+6与x轴交于点A，与y轴交于点B，将直线l₁向下平移4个单位长度后得到直线l₂，直线l₂与x轴交于点C，与y轴交于点D．

（1）求△AOB的面积；
（2）直线l₂的函数表达式是___．
（3）若点P是折线CAB上一点，且S_△PBD= (1)/(2)S_{四边形ABCD}，请求点P的坐标．

Answer 1

（1）当x=0时，y=-(3)/(4)x+6=6，
∴点B的坐标为（0，6）；
当y=-(3)/(4)x+6=0时，x=8，
∴点A的坐标为（8，0）．
∴S_△AOB=(1)/(2)OA•OB=(1)/(2)×8×6=24．
（2）∵将直线l₁向下平移4个单位长度后得到直线l₂，
∴直线l₂的函数表达式是y=-(3)/(4)x+6-4=-(3)/(4)x+2．
故答案为：y=-(3)/(4)x+2．
（3）当x=0时，y=-(3)/(4)x+2=2，
∴点D的坐标为（0，2）；
当y=-(3)/(4)x+2=0时，x=(8)/(3)，
∴点C的坐标为（(8)/(3)，0）．
∴S_{四边形ABCD}=S_△AOB-S_△COD=24-(1)/(2)×2×(8)/(3)=(64)/(3)．
设点P的横坐标为m（0<m≤8），
∵S_△PBD=(1)/(2)S_{四边形ABCD}，
∴BD•m=（6-2）m=(64)/(3)，
解得：m=(16)/(3)，
∵(8)/(3)<(16)/(3)<8，且当x=(16)/(3)时，y=-(3)/(4)x+6=-(3)/(4)×(16)/(3)+6=2，
∴点P的坐标为（(16)/(3)，0）和（(16)/(3)，2）．