早教吧作业答案频道 -->数学-->
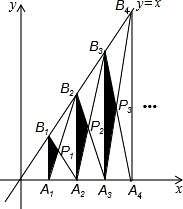
如图,已知A1,A2,…,An,An+1在x轴上,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,…,An,An+1作x轴的垂线交直线y=x于点B1,B2,…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3,…,AnBn+1,BnAn+1,依次
题目详情
如图,已知A1,A2,…,An,An+1在x轴上,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,…,An,An+1作x轴的垂线交直线y=x于点B1,B2,…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn,△A1B1P1,△A2B2P2,…,△AnBnPn的面积依次为S1,S2,…,Sn,则S1=___,Sn=___.

▼优质解答
答案和解析
 ∵A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=x于点B1、B2、B3、…、Bn、Bn+1,
∵A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=x于点B1、B2、B3、…、Bn、Bn+1,
∴依题意得:B1(1,1),B2(2,2),B3(3,3),…,Bn(n,n)
∵A1B1∥A2B2,
∴△A1B1P1∽△A2B2P1,
∴
=
,
∴△A1B1P1与△A2B2P1对应高的比为:1:2,
∵A1A2=1,
∴A1B1边上的高为:
,
∴S △A1B1P1=
×1×
=
,
同理可得:S △A2B2P2=
,S△A3B3P3=
,
∴Sn=
.
故答案为
、
.
 ∵A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=x于点B1、B2、B3、…、Bn、Bn+1,
∵A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=x于点B1、B2、B3、…、Bn、Bn+1,∴依题意得:B1(1,1),B2(2,2),B3(3,3),…,Bn(n,n)
∵A1B1∥A2B2,
∴△A1B1P1∽△A2B2P1,
∴
| A 1B1 |
| A2B2 |
| 1 |
| 2 |
∴△A1B1P1与△A2B2P1对应高的比为:1:2,
∵A1A2=1,
∴A1B1边上的高为:
| 1 |
| 3 |
∴S △A1B1P1=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
同理可得:S △A2B2P2=
| 2 |
| 5 |
| 9 |
| 14 |
∴Sn=
| n2 |
| 4n+2 |
故答案为
| 1 |
| 6 |
| n2 |
| 4n+2 |
看了 如图,已知A1,A2,…,A...的网友还看了以下:
设集合A={1,3,a}B={1,a²-a+1}且A=B,求a的值设集合A={1,a}B={1,a 2020-04-05 …
已知数列{an},a1=1且满足an=a(n-1)+2n-1(n≥2),求数列{an}的通项公式a 2020-05-13 …
已知两个复数Z1=1+i,Z2=21+28i,数列{an}的通项公式an=nZ1-1,且前n项和S 2020-05-13 …
已知两个复数z1=1+i,z2=21+28i,数列an的通项公式为an=nz1-1,且前n项的和为 2020-05-13 …
高中数学题目 帮忙一下 哥哥姐姐们等差数列{an}中,前n项和Sn=an^+(a-1)n+(a 2020-05-16 …
已知数列{an}满足(1/1-an+1)-(1/1-an)=1,且a1=0(1)求数列{an}的通 2020-05-17 …
不等式证明!在线等(与数列有关)求证an>1数列{an}中,已知a1=a(a>1),且an+1=( 2020-07-29 …
1.已知集合A={x|x²-1=0},选用适当的符号填空:1A{-1}A空集A{1,-1}A2.设 2020-07-30 …
若正项等比数列{an}的公比a≠1,且a4,2a5,a6成等差数列,则a3+a5/a4+a6= 2020-07-30 …
设A1=2,An+1=1/2[An+(1/An)],求An是否收敛?注:不会弄下标,所以小写代表下标 2020-11-18 …