四边形ABCD是正方形，△CEF是等腰直角三角形，∠CEF=90°，EF=EC，连接AF，G为AF的中点，连接GB，GE，EB（1）如图①，当点B、C、E在同一直线上时，求证：GB⊥GE（方法提示：可以延长BG…构造

Question

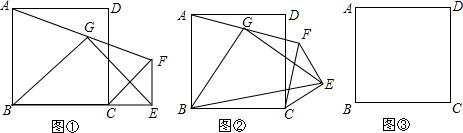
四边形ABCD是正方形，△CEF是等腰直角三角形，∠CEF=90°，EF=EC，连接AF，G为AF的中点，连接GB，GE，EB
（1）如图①，当点B、C、E在同一直线上时，求证：GB⊥GE（方法提示：可以延长BG…构造全等三角形进行证明，方法不唯一，仅供参考）
（2）将图①中的△CEF绕点C逆时针旋转至图②位置时，GB与CE是否垂直？若垂直，请写出证明过程：若不垂直，请说明理由
（3）将图③中的△CEF绕点C逆时针旋转一周，若CE=3，AB=3 √(2)，点E，F，A三点共线时，∠DCF=___°（直接写出结果）

Answer 1

（1）证明：过G作GH⊥BE于H，如图1所示：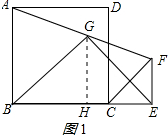
∵∠CEF=∠ABC=90°，
∴EF∥GH∥AB，
∵G为AF中点，
∴H为BE中点，
∴GH是梯形ABEF的中位线，GB=GE，
∴GH=(1)/(2)（EF+AB）=(1)/(2)（CE+BC），
即GH=EH=HB，
∴△GBH和△GEH是等腰直角三角形，
∴∠BGH=∠EGH=45°，
∴∠BGE=90°，
∴GB⊥GE；
（2） GB⊥GE，理由如下：
延长EG到H，使EG=GH，连接BH、AH，过E作BC的垂线EM，交CB延长线于R、交DF延长线于M，延长BA交GH于N，如图2所示：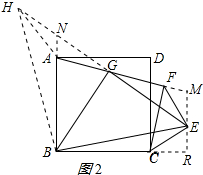
在△EFG和△HAG中，

AG=GF

∠FGE=∠AGH

EG=GH

，
∴△EFG≌△HAG（SAS），
∴AH=EF=CE，∠FEG=∠AHG，
∴EF∥DH，
∵EM⊥BC，
∴EM∥AB∥DN，
∴∠HAN=∠FEM，
∵∠FEM+∠CER=90°，
∠ECR+∠CER=90°，
∴∠FEM=∠ECR，
∴∠HAN=∠ECR，
∴∠BAH=∠BCE，
在△EBC和△HAB中，

AB=BG

∠BCE=∠BAH

AH=CE

，
∴△EBC≌△HAB（SAS），
∴BE=BH，∠CBE=∠ABH，
∴∠EBH=∠ABH+∠ABE=∠CBE+∠ABE=∠ABC=90°，
∴△BEH是等腰直角三角形，
∵G为EH的中点，
∴GB⊥GE；
（3） 连接AC，如图3所示：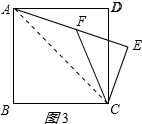
∵AB=3√(2)，四边形ABCD是正方形，
∴AC=√(2)AB=6，
∴cos∠ACE=(CE)/(AC)=(3)/(6)=(1)/(2)，
∴∠ACE=60°，
∴∠DCE=∠ACE-∠ACD=15°，
∴∠DCF=45°-15°=30°，
故答案为：30．