早教吧作业答案频道 -->数学-->
如图,△ABC中,AB=AC=2,∠BAC=45°,将△ABC绕点A按顺时针方向旋转角α得到△AEF,且0°<α≤180°,连接BE、CF相交于点D.(1)求证:BE=CF;(2)当α=90°时,求四边形AEDC的面积.
题目详情
如图,△ABC中,AB=AC=2,∠BAC=45°,将△ABC绕点A按顺时针方向旋转角α得到△AEF,且0°<α≤180°,连接BE、CF相交于点D.
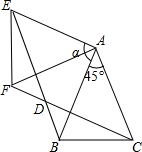
(1)求证:BE=CF;
(2)当α=90°时,求四边形AEDC的面积.

(1)求证:BE=CF;
(2)当α=90°时,求四边形AEDC的面积.
▼优质解答
答案和解析
(1)证明:∵△ABC绕点A按顺时针方向旋转角α得到△AEF,
∴AE=AB,AF=AC,∠EAC=∠BAC,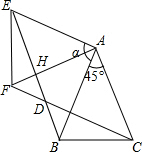
∴AB=AC=AE=AF,∠EAF+∠FAB=∠BAC+∠FAB,即∠EAB=∠FAC,
在△AEB和△AFC中,
,
∴△AEB≌△AFC,
∴BE=CF;
(2) ∵α=90°,即∠EAB=∠FAC=90°,
∵AE=AB,
∴△ABE为等腰直角三角形,
∴∠ABE=45°,
∴∠ABE=∠BAC,
∴AC∥BE,
同理可得AE∥CF,
∵AE=AC,
∴四边形AEDC为菱形,
AF与BE交于点H,如图,
∵∠EAF=45°,
∴AH平分∠EAB,
∴AH⊥BE,
∴△AHE为等腰直角三角形,
∴AH=
AE=
,
∴四边形AEDC的面积=AH•DE=
×2=2
.
∴AE=AB,AF=AC,∠EAC=∠BAC,

∴AB=AC=AE=AF,∠EAF+∠FAB=∠BAC+∠FAB,即∠EAB=∠FAC,
在△AEB和△AFC中,
|
∴△AEB≌△AFC,
∴BE=CF;
(2) ∵α=90°,即∠EAB=∠FAC=90°,
∵AE=AB,
∴△ABE为等腰直角三角形,
∴∠ABE=45°,
∴∠ABE=∠BAC,
∴AC∥BE,
同理可得AE∥CF,
∵AE=AC,
∴四边形AEDC为菱形,
AF与BE交于点H,如图,
∵∠EAF=45°,
∴AH平分∠EAB,
∴AH⊥BE,
∴△AHE为等腰直角三角形,
∴AH=
| ||
| 2 |
| 2 |
∴四边形AEDC的面积=AH•DE=
| 2 |
| 2 |
看了 如图,△ABC中,AB=AC...的网友还看了以下:
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
(b-a)x平方+(a-c)+c-b=0(a不等于b) 2020-05-16 …
对于90℃的纯水,以下认识正确的是()A.c(H+)>10-7mol/L>c(OH-)pH<7显中 2020-06-23 …
若(2x-1)的三次方=a+bx+cx平方+dx立方,要求a+b+c+d的值可令x=1,原等式变为 2020-07-30 …
(a+b-c)(a+b+c)为什么可以(a+b)的平方-c的平方啊?不是只有a+b+c才能变成(a 2020-07-31 …
初二勾股定理阅读下列解题过程:已知a,b,c为三角形ABC的三边,且满足a方c方-b方c方=a的四 2020-08-02 …
下表为周期表中短周期的一部分.已知a原子的最外层电子数是电子总数的三分之一,下列说法中正确的是()A 2020-11-02 …
100%收购公司其中一名法人股东涉及到的问题事实:A.B.C.D为四个法人。A.B公司为C公司的股东 2020-11-06 …
1+a四方小于等于2乘以b-c括号平方,1+b四方小于等于2乘以c-a括号平方,1+c四方小于等于2 2020-11-07 …
在三角形ABC和三角形A'B'C'中CD,C'D'分别是高,并且AC=A'C;,CD=C'D',∠A 2020-11-28 …