如图，在平面直角坐标系xOy中，抛物线y=x2-（1-m）x+3m经过点A（-1，0），且与y轴相交于点B．（1）求这条抛物线的表达式及点B的坐标；（2）设点C是所求抛物线上一点，线段BC与x轴正半轴相

Question

如图，在平面直角坐标系xOy中，抛物线y=x²-（1-m）x+3m经过点A（-1，0），且与y轴相交于点B．

（1）求这条抛物线的表达式及点B的坐标；
（2）设点C是所求抛物线上一点，线段BC与x轴正半轴相交于点D，如果(BD)/(CD)=(3)/(5)，求点C的坐标；
（3）在（2）条件下，联结AC，求∠ABC的度数．

Answer 1

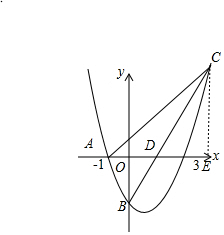（1）把A（-1，0）代入y=x²-（1-m）x+3m得：0=（-1）²+（1-m）+3m，
解得：m=-1，
∴抛物线的表达式y=x²-2x-3，当x=0时，y=-3，
∴B的坐标为（0，-3）；
（2）过C作CE⊥x轴于E，则CE∥y轴，
∴△BDO∽△CDE，
∴(BD)/(CD)=(BO)/(CE)=(OD)/(DE)，即(OD)/(DE)=(3)/(CE)=(3)/(5)，
∴CE=5，
把y=5代入y=x²-2x-3得：x₁=-2（舍去），x₂=4，
∴C（4，5）；
（3）解方程x²-2x-3=0得：x₁=-1，x₂=3，
∴A（-1，0），
∵B（0，-3），C（4，5），
∴AC²=（4+1）²+5²=50，
∵(OD)/(DE)=(3)/(5)，OD+DE=4，
∴DE=(5)/(2)，
∴DC=√(((5)/(2))2+52)=(5√(5))/(2)，BC=√((5+3)2+42)=4√(5)，
∴DC•BC=50，
∴AC²=DC•BC，
∵∠ACD=∠BCA，
∴△CDA∽△CBA，
∴∠ABC=∠CAD，
∵CE=AE=5，
∴∠CAD=45°，
∴∠ABC=45°．