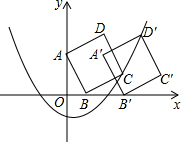
如图，在平面直角坐标系中，正方形ABCD的顶点A，B的坐标分别为（0，2），（1，0），顶点C在函数y=13x2+bx-1的图象上，将正方形ABCD沿x轴正方形平移后得到正方形A′B′C′D

Question

如图，在平面直角坐标系中，正方形ABCD的顶点A，B的坐标分别为（0，2），（1，0），顶点C在函数y= (1)/(3)x²+bx-1的图象上，将正方形ABCD沿x轴正方形平移后得到正方形A′B′C′D′，点D的对应点D′落在抛物线上，则点D与其对应点D′间的距离为___．

Answer 1

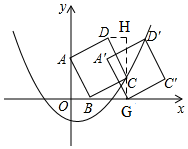如图，过C作GH⊥x轴，交x轴于G，过D作DH⊥GH于H，
∵A（0，2），B（1，0），
∴OA=2，OB=1，
∵四边形ABCD为正方形，
∴∠ABC=90°，AB=BC，
∴∠ABO+∠CBG=90°，
∵∠ABO+∠OAB=90°，
∴∠CBG=∠OAB，
∵∠AOB=∠BGC=90°，
∴△AOB≌△BGC，
∴BG=OA=2，CG=OB=1，
∴C（3，1），
同理得：△BCG≌△CDH，
∴CH=BG=2，DH=CG=1，
∴D（2，3），
∵C在抛物线的图象上，
把C（3，1）代入函数y=(1)/(3)x²+bx-1中得：b=-(1)/(3)，
∴y=(1)/(3)x²-(1)/(3)x-1，
设D（x，y），
由平移得：D与D′的纵坐标相同，则y=3，
当y=3时，(1)/(3)x²-(1)/(3)x-1=3，
解得：x₁=4，x₂=-3（舍），
∴DD′=4-2=2，
则点D与其对应点D′间的距离为2，
故答案为：2．