早教吧作业答案频道 -->数学-->
已知△ABC和△CDE中,CA=CB,CD=CE,∠ACB=∠DCE=α,AE与BD交于点F.(1)如图1.当α=90°时.求证:①△ACE≌△BCD;②AE⊥BD;(2)如图2.当α=60°时,直接写出∠AFB的度数为;(3)如图3,
题目详情
已知△ABC和△CDE中,CA=CB,CD=CE,∠ACB=∠DCE=α,AE与BD交于点F.
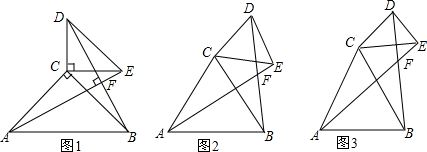
(1)如图1.当α=90°时.求证:①△ACE≌△BCD;②AE⊥BD;
(2)如图2.当α=60°时,直接写出∠AFB的度数为___;
(3)如图3,直接写出∠AFD的度数为___ (用含α的式子表示).
(1)如图1.当α=90°时.求证:①△ACE≌△BCD;②AE⊥BD;
(2)如图2.当α=60°时,直接写出∠AFB的度数为___;
(3)如图3,直接写出∠AFD的度数为___ (用含α的式子表示).

▼优质解答
答案和解析
证明:(1)∵∠ACB=∠DCE=90°,
∴∠ACB-∠ACD=∠DCE-∠ACD,
即∠ACE=∠BCD,
又∵△ABC和△ECD都是等腰直角三角形
∴AC=BC,EC=DC,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴∠CAE=∠CBD,
∵∠CAE+∠EAB+∠ABC=90°,
∴∠CBD+∠EAB+∠ABC=90°,
∴∠AFB=90°,
∴AE⊥BD;
(2)∵∠ACB=∠DCE=60°,
∴∠ACB-∠ACD=∠DCE-∠ACD,
即∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴∠CAE=∠CBD,
∴A,B,F,C四点共圆,
∴∠AFB=∠ACB=60°;
故答案为:60°;
(3))∵∠ACB=∠DCE=α,
∴∠ACB-∠ACD=∠DCE-∠ACD,
即∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴∠CAE=∠CBD,
∴A,B,F,C四点共圆,
∴∠AFB=∠ACB=α,
∴∠AFD=180°-α.
故答案为:180°-α.
∴∠ACB-∠ACD=∠DCE-∠ACD,
即∠ACE=∠BCD,
又∵△ABC和△ECD都是等腰直角三角形
∴AC=BC,EC=DC,
在△ACE和△BCD中,
|
∴△ACE≌△BCD(SAS),
∴∠CAE=∠CBD,
∵∠CAE+∠EAB+∠ABC=90°,
∴∠CBD+∠EAB+∠ABC=90°,
∴∠AFB=90°,
∴AE⊥BD;
(2)∵∠ACB=∠DCE=60°,
∴∠ACB-∠ACD=∠DCE-∠ACD,
即∠ACE=∠BCD,
在△ACE和△BCD中,
|
∴△ACE≌△BCD(SAS),
∴∠CAE=∠CBD,
∴A,B,F,C四点共圆,
∴∠AFB=∠ACB=60°;
故答案为:60°;
(3))∵∠ACB=∠DCE=α,
∴∠ACB-∠ACD=∠DCE-∠ACD,
即∠ACE=∠BCD,
在△ACE和△BCD中,
|
∴△ACE≌△BCD(SAS),
∴∠CAE=∠CBD,
∴A,B,F,C四点共圆,
∴∠AFB=∠ACB=α,
∴∠AFD=180°-α.
故答案为:180°-α.
看了 已知△ABC和△CDE中,C...的网友还看了以下:
提示:D-C=0A-B,A-D,D-C,D-E,E-F=1A-D,C-F=2A-B,D-E,E-F 2020-04-06 …
A、B、C、D、E、F六种元素,其中ABCDE为短周期元素,①原子半径A<C<B<E<D②原子最外 2020-05-13 …
A.{A}{A,B,C,D,E}{A,B,C,D,E,F,G,H,I,J,K}B.{F}{G}{H} 2020-05-26 …
设矩阵A,B满足A=E(1,3)E(5(-2))BE(3,2(1/2)),则有A.B=E(1,3) 2020-06-28 …
设一数列a,b,c,d,e,f,通过栈结构不可能不可能排成的顺序数列为()A)c,b,e,f,d, 2020-06-28 …
#include"stdio.h"main(){inta,b,c,e;printf(“please 2020-07-23 …
ASP数组str="a,b,c,d,e,f"我要依次得到a+b,a+b+c,a+b+c+d,a+b 2020-07-29 …
若a,b,c,d都是整数,其中c大于0,并且满足a+b+c=d,b+c+d=e,c+d+e=a,e 2020-07-30 …
代数化简法化简1.L=A*B*非C+非(A*B*C)*非(A*B)1.L=A*B*非C+非(A*B* 2020-12-07 …
设A是3*4的矩阵,C=(B-E)A.其中B为[32-1,-230,000],求秩A和C的关系 2021-02-10 …