早教吧作业答案频道 -->数学-->
如图,在等腰直角三角形MNC中.CN=MN=2,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.(1)∠NCO的度数为;(2)求证:△CAM为等边三
题目详情
如图,在等腰直角三角形MNC中.CN=MN=
,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
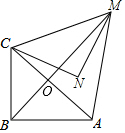
(1)∠NCO的度数为___;
(2)求证:△CAM为等边三角形;
(3)连接AN,求线段AN的长.
| | 2 |

(1)∠NCO的度数为___;
(2)求证:△CAM为等边三角形;
(3)连接AN,求线段AN的长.
▼优质解答
答案和解析
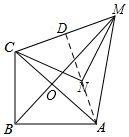 (1)由旋转可得∠ACM=60°,
(1)由旋转可得∠ACM=60°,
又∵等腰直角三角形MNC中,∠MCN=45°,
∴∠NCO=60°-45°=15°;
故答案为:15°;
(2)∵∠ACM=60°,CM=CA,
∴△CAM为等边三角形;
(3)连接AN并延长,交CM于D,
∵△MNC是等腰直角三角形,△ACM是等边三角形,
∴NC=NM=
,CM=2,AC=AM=2,
在△ACN和△AMN中,
,
∴△ACN≌△AMN(SSS),
∴∠CAN=∠MAN,
∴AD⊥CM,CD=
CM=1,
∴Rt△ACD中,AD=
CD=
,
等腰Rt△MNC中,DN=
CM=1,
∴AN=AD-ND=
-1.
 (1)由旋转可得∠ACM=60°,
(1)由旋转可得∠ACM=60°,又∵等腰直角三角形MNC中,∠MCN=45°,
∴∠NCO=60°-45°=15°;
故答案为:15°;
(2)∵∠ACM=60°,CM=CA,
∴△CAM为等边三角形;
(3)连接AN并延长,交CM于D,
∵△MNC是等腰直角三角形,△ACM是等边三角形,
∴NC=NM=
| 2 |
在△ACN和△AMN中,
|
∴△ACN≌△AMN(SSS),
∴∠CAN=∠MAN,
∴AD⊥CM,CD=
| 1 |
| 2 |
∴Rt△ACD中,AD=
| 3 |
| 3 |
等腰Rt△MNC中,DN=
| 1 |
| 2 |
∴AN=AD-ND=
| 3 |
看了 如图,在等腰直角三角形MNC...的网友还看了以下:
如图是曲柄连杆机构的示意图,当曲柄CB绕点C旋转时,通过连杆AB的传递,活塞作直线往复运动.当曲柄 2020-05-17 …
如图,已知点A(2,0),点B在y轴正半轴上,且OB=1/2OA,将点B绕点A顺时针方向旋转90度 2020-06-13 …
已知,在等腰三角形ABC中,AB=AC,角BAC=90°,将△ABC绕点C旋转45°,成为RT△C 2020-06-25 …
如图所示的四件展品展现了我国古代劳动人民的智慧成果,对其中所涉及的物理知识,下列说法中正确的是() 2020-07-05 …
已知:在△ABC中,∠BAC=60°.(1)如图1,若AB=AC,点P在△ABC内,且∠APC=1 2020-07-17 …
如图,在△ABC和△DCE中,AC=BC,DC=EC,∠ACB=∠DCE=90°,将△DCE绕点C 2020-07-27 …
正方形ABCD和正方形CEFG,M为AF的中点,连接MD、ME.(1)如图,B、C、G依次在同一条 2020-08-03 …
如图,在Rt△ABC中,∠B=90°,AB=2根号3,∠C=60°,将△ABC绕点A逆时针旋转得到△ 2020-12-21 …
(2012•湛江一模)如图是曲柄连杆机构的示意图,当曲柄CB绕点C旋转时,通过连杆AB的传递,活塞作 2021-01-14 …
初三几何综合在RT△ABC中,∠ACB=90°,tan∠BAC=1/2,点D在边AC上,不与A,C重 2021-02-04 …