早教吧作业答案频道 -->数学-->
如图,AB是O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交AC于点F,交过点C的切线于点D.(1)求证:DC=DP;(2)若∠CAB=30°,当F是AC的中点时,判断以A,O
题目详情
如图,AB是 O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交
于点F,交过点C的切线于点D.
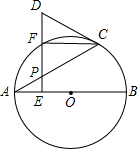
(1)求证:DC=DP;
(2)若∠CAB=30°,当F是
的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
 |
| AC |

(1)求证:DC=DP;
(2)若∠CAB=30°,当F是
 |
| AC |
▼优质解答
答案和解析
(1)证明:连接OC,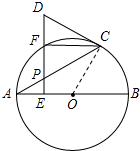
∵∠OAC=∠ACO,PE⊥OE,OC⊥CD,
∴∠APE=∠PCD,
∵∠APE=∠DPC,
∴∠DPC=∠PCD,
∴DC=DP;
(2) 以A,O,C,F为顶点的四边形是菱形;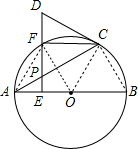
∵∠CAB=30°,∴∠B=60°,
∴△OBC为等边三角形,
∴∠AOC=120°,
连接OF,AF,
∵F是
的中点,
∴∠AOF=∠COF=60°,
∴△AOF与△COF均为等边三角形,
∴AF=AO=OC=CF,
∴四边形OACF为菱形.

∵∠OAC=∠ACO,PE⊥OE,OC⊥CD,
∴∠APE=∠PCD,
∵∠APE=∠DPC,
∴∠DPC=∠PCD,
∴DC=DP;
(2) 以A,O,C,F为顶点的四边形是菱形;

∵∠CAB=30°,∴∠B=60°,
∴△OBC为等边三角形,
∴∠AOC=120°,
连接OF,AF,
∵F是
 |
| AC |
∴∠AOF=∠COF=60°,
∴△AOF与△COF均为等边三角形,
∴AF=AO=OC=CF,
∴四边形OACF为菱形.
看了 如图,AB是O的直径,点P是...的网友还看了以下:
直线AB过点A(m,0)、B(0,n)(m>0,n>0),反比例函数y=m/x的图像与AB交于C、 2020-04-08 …
已知点A(-2,0),B(2,0),曲线c上动点P满足ap向量·bp向量=-3.(1)曲线C的方程 2020-05-16 …
已知点A(—2,0),B(2,0),曲线C上动点P满足向量AP乘以向量BP=—3(1)曲线C的方程 2020-05-16 …
已知下列命题:①若a>0,b>0,则a+b>0;②若a≠b,则a2≠b2;③两点之间,线段最短;④ 2020-05-17 …
已知抛物线经过A(-2,0)B(1,0)C(0,2)三点……已知抛物线经过A(-2,0)B(1,0 2020-06-06 …
已知圆x2+y2+2ax-2ay+2a2-4a=0(0<a≤4)的圆心为C,直线l:y=x+m.( 2020-06-09 …
已知直线y=0.5x与双曲线y=k/x(k>0)交与A,B两点,且点A的横坐标为4.已知直线y=0 2020-06-14 …
已知直线l1:x+ay+1=0,直线l2:ax+y+2=0,则命题“若a=1或a=-1,则直线l1 2020-07-09 …
直线l的一般方程为:Ax+By+C=0,其中A,B不同时为0若B不为0,则直线l的斜率为,在y轴上 2020-07-13 …
已知抛物线y=3ax^2+2bx+c1.若a=b=1,且—1<x<1时抛物线与x轴有且只有一个公共点 2020-11-01 …