早教吧作业答案频道 -->数学-->
如图,AB是O的直径,BD交O于点C,E为BC的中点,连接AE交BD于点F,作FG⊥AB,垂足为G,连接AD,且∠D=2∠BAE.(1)求证:AD为O的切线;(2)若cosD=35,AD=6,求FG的长.
题目详情
如图,AB是 O的直径,BD交 O于点C,E为 BC 的中点,连接AE交BD于点F,作FG⊥AB,垂足为G,连接AD,且∠D=2∠BAE.
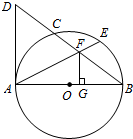
(1)求证:AD为 O的切线;
(2)若cosD=
,AD=6,求FG的长.

(1)求证:AD为 O的切线;
(2)若cosD=
| 3 |
| 5 |
▼优质解答
答案和解析
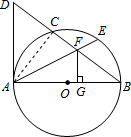 (1)证明:连接AC,
(1)证明:连接AC,
∵AB是 O的直径,
∴∠ACB=90°,
∴∠ABC+∠BAC=90°,
∵E为
的中点,
∴∠BAE=∠CAE,
∴∠BAC=2∠BAE,
∵∠D=2∠BAE,
∴∠BAC=∠D,
∴∠ABC+∠D=90°,
∴∠BAD=90°,
∴BA⊥AD,
∴AD为 O的切线;
(2)∵cosD=
,AD=6,
∴sinD=
,BD=
=
=10,
∴AC=AD•sinD=6×
=
,AB=
=8,
在△FAG和△FAC中
∴△FAG≌△FAC(AAS),
∴AG=AC=
,
∴BG=8-
=
,
∵FG⊥AB,DA⊥AB,
∴FG∥DA,
∴△BFG∽△BDA,
∴
=
,即
=
,
∴FG=
.
 (1)证明:连接AC,
(1)证明:连接AC,∵AB是 O的直径,
∴∠ACB=90°,
∴∠ABC+∠BAC=90°,
∵E为
 |
| BC |
∴∠BAE=∠CAE,
∴∠BAC=2∠BAE,
∵∠D=2∠BAE,
∴∠BAC=∠D,
∴∠ABC+∠D=90°,
∴∠BAD=90°,
∴BA⊥AD,
∴AD为 O的切线;
(2)∵cosD=
| 3 |
| 5 |
∴sinD=
| 4 |
| 5 |
| AD |
| cosD |
| 6 | ||
|
∴AC=AD•sinD=6×
| 4 |
| 5 |
| 24 |
| 5 |
| BD2-AD2 |
在△FAG和△FAC中
|
∴△FAG≌△FAC(AAS),
∴AG=AC=
| 24 |
| 5 |
∴BG=8-
| 24 |
| 5 |
| 16 |
| 5 |
∵FG⊥AB,DA⊥AB,
∴FG∥DA,
∴△BFG∽△BDA,
∴
| FG |
| AD |
| BG |
| AG |
| FG |
| 6 |
| ||
| 8 |
∴FG=
| 12 |
| 5 |
看了 如图,AB是O的直径,BD交...的网友还看了以下:
抛物线..抛物线C1:y=-X^2+2mx+n(m.n为常数,且m不=0,n>0)的顶点为A,与Y 2020-04-27 …
和例句句式相同的一项是[]例:如诗不成,罚依金谷酒数A.夫天地者万物B.大块假我以文章C.群季俊秀 2020-06-23 …
如图,CB、CD是⊙O的切线,切点分别为B、D.CD的延长线与⊙O的直径BE的延长线交于A点,连接 2020-07-24 …
如图,点A、C为反比例函数y=kx(x<0)图象上的点,过点A、C分别作AB⊥x轴,CD⊥x轴,垂 2020-07-24 …
如图已知点A的坐标(根号3,3)AB⊥X轴,垂足为B,连接CA,反比例函数y=k/x(k>0)与线 2020-07-31 …
如图所示,已知回旋加速器的匀强磁场的磁感应强度为B,D形金属盒的半径为R,狭缝间的距离为d,加在两D 2020-12-09 …
(2014•黄浦区二模)图为两个相干波源发出的波相遇时的情况,实线表示波峰,虚线表示波谷.相干波的振 2020-12-15 …
图为两个相干波源发出的波相遇时的情况,实线表示波峰,虚线表示波谷.相干波的振幅均为5cm,波速和波长 2020-12-15 …
如图为回旋加速器的装置图,D型盒的两底边分别为a、b,且相距很近,忽略粒子在其间的运动时间,设D型盒 2021-01-17 …
如图所示,已知回旋加速器的匀强磁场的磁感应强度为B,D形金属盒的半径为R,狭缝间的距离为d,加在两D 2021-01-17 …