早教吧作业答案频道 -->数学-->
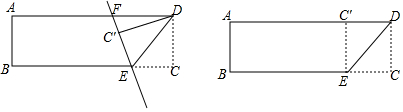
己知:一张矩形纸片记作矩形ABCD,CD=3,AD=8,点E是边BC上的点,连结DE,将△DEC沿着DE所在的直线折叠,记点C的对称点为点C′,C′E所在的直线交边AD于点F,设EC=x.(1)若点C′恰好落在边AD
题目详情
己知:一张矩形纸片记作矩形ABCD,CD=3,AD=8,点E是边BC上的点,连结DE,将△DEC沿着DE所在的直线折叠,记点C的对称点为点C′,C′E所在的直线交边AD于点F,设EC=x.
(1)若点C′恰好落在边AD上,求x的值.
(2)①若点C′落在矩形ABCD内部,求证:△FED是等腰三角形.
②当△FED是等边三角形时,x=___(直接写出答案)
(3)当x=6时,△FED的面积=___(直接写出答案)
(1)若点C′恰好落在边AD上,求x的值.
(2)①若点C′落在矩形ABCD内部,求证:△FED是等腰三角形.
②当△FED是等边三角形时,x=___(直接写出答案)
(3)当x=6时,△FED的面积=___(直接写出答案)

▼优质解答
答案和解析
(1)如图1中,
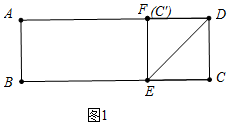
点C′恰好落在边AD上时,
∵四边形ABCD是矩形,
∴∠C=∠ADC=90°,
由折叠的性质可知∠EDC=∠EDF=45°,
∵∠C=∠EC′D=90°,
∴△DEC′,△DEC都是等腰直角三角形,
∴x=EC=CD=3,
(2)①如图2中,
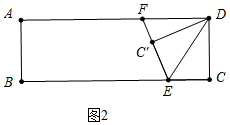
点C′落在矩形ABCD内部时,∵∠DEC=∠DEC′,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠FDE=∠DEC,
∴∠FED=∠FDE,
∴FE=FD,
∴△DEF是等腰三角形.
②如图3,
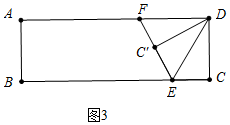
∵△DEF是等边三角形,
∴∠FDE=60°,
∴∠EDC=90°-∠FDE=30°,
在Rt△DEC中,EC=DC•tan30°=3×
=
.
∴x=
,
故答案为
.
(3)如图4中,作EM⊥AD于M.
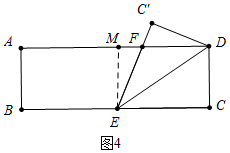
∵∠CED=∠DEF=∠FDE,
∴FE=FD,设FE=FD=x,
在Rt△DEM中,∵FM=DM-DF=EC-DF=6-x,EM=CD=3,
∴32+(6-x)2=x2,
∴x=
,
∴EF=
,
∴S△EFD=
•EF•DC′=
×
×3=
.
故答案为
.

点C′恰好落在边AD上时,
∵四边形ABCD是矩形,
∴∠C=∠ADC=90°,
由折叠的性质可知∠EDC=∠EDF=45°,
∵∠C=∠EC′D=90°,
∴△DEC′,△DEC都是等腰直角三角形,
∴x=EC=CD=3,
(2)①如图2中,

点C′落在矩形ABCD内部时,∵∠DEC=∠DEC′,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠FDE=∠DEC,
∴∠FED=∠FDE,
∴FE=FD,
∴△DEF是等腰三角形.
②如图3,

∵△DEF是等边三角形,
∴∠FDE=60°,
∴∠EDC=90°-∠FDE=30°,
在Rt△DEC中,EC=DC•tan30°=3×
| ||
| 3 |
| 3 |
∴x=
| 3 |
故答案为
| 3 |
(3)如图4中,作EM⊥AD于M.

∵∠CED=∠DEF=∠FDE,
∴FE=FD,设FE=FD=x,
在Rt△DEM中,∵FM=DM-DF=EC-DF=6-x,EM=CD=3,
∴32+(6-x)2=x2,
∴x=
| 15 |
| 4 |
∴EF=
| 15 |
| 4 |
∴S△EFD=
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 4 |
| 45 |
| 8 |
故答案为
| 45 |
| 8 |
看了 己知:一张矩形纸片记作矩形A...的网友还看了以下:
已知,,圆,一动圆在轴右侧与轴相切,同时与圆相外切,此动圆的圆心轨迹为曲线C,曲线E是以,为焦点的 2020-05-15 …
已知曲线C的方程为y2=4x(x>0),曲线E是以F1(-1,0)、F2(1,0)为焦点的椭圆,点 2020-05-15 …
如图,四边形ABCD是平行四边形,点E、F分别为AD、BC边上的点,且AE=CF求证:四边形BED 2020-05-16 …
如右图所示,一只老鼠沿着平行四边形ADC方向逃跑:同时,一只猫也从A出发沿着ABC的方向抓捕老鼠. 2020-05-17 …
如图1,已知点P是线段AB上的动点(P不与A,B重合),分别以AP、PB为边向线段AB的同一侧作等 2020-06-08 …
当windows中窗口被最大化后,如果想要调整窗口的大小,应进行的操作A、鼠标拖动窗口的边框线B、 2020-07-12 …
如图,点B在线段AF上,分别以AB、BF为边在线段AF的同侧作正方形ABCD和正方形BFGE,连接 2020-07-21 …
急问一物理题图我就不画了,就是一条直线,线上有两点,左边为A点,右边为B点再由此点电荷产生的电场中的 2020-10-30 …
已知△ABC中,AD为BC边中线,E为AD上一点,并且CE=CD,∠EAC=∠B,求证△AEC∽△B 2020-12-05 …
曲线y=e的(1/2*x)在点(4,e*e)处的切线与坐标轴所围成的三角形的面积是?还有,y=e的( 2021-02-07 …