已知函数f(x)与函数y=(a＞0)的图象关于直线y=x对称.(1)试用含a的代数式表示函数f(x)的解析式，并指出它的定义域；(2)数列{an}中，a1=1，当n≥2时，an＞a1.数列{bn}中，b1=2，Sn

Question

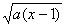已知函数f(x)与函数y= (a＞0)的图象关于直线y=x对称.

(1)试用含a的代数式表示函数f(x)的解析式，并指出它的定义域；

(2)数列{a _n }中，a ₁ =1，当n≥2时，a _n ＞a ₁ .数列{b _n }中，b ₁ =2，S _n =b ₁ +b ₂ +…+b _n .点P _n (a _n 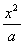) (n=1 2 3 …)在函数f(x)的图象上，求a的值；

(3)在(2)的条件下，过点P _n 作倾斜角为 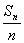的直线l _n ，则l _n 在ｙ轴上的截距为 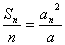(b _n +1)(n=1 2 3 …)，求数列{a _n }的通项公式.

Answer 1

(1)由题可知：f(x)与函数y=(a＞0)互为反函数，∴f(x)=+1，(x≥0).   (2)∵点Pn(an )(n=1 2 3 …)在函数f(x)的图象上，∴+1(n=1 2 3 …)(*)在上式中令n=1可得：S1=+1，又∵a1=1 S1=b1=2，代入可解得：a=1.∴f(x)=x2+1，(*)式可化为：=an2+1(n=1 2 3 …).                                                 (3)直线ln的方程为：y=x-an，(n=1 2 3 …)，①在其中令x=0，得y=-an，又∵ln在ｙ轴上的截距为(bn+1)，∴-an=(bn+1)，结合①式可得：bn=3an2-3an+2.                                                          ②由①可知：当自然数n≥2时，Sn=nan2+n，Sn-1=(n-1)an-12+n-1，两式作差得：bn=nan2-(n-1)an-12+1结合②式得：(n-3)an2+3an=(n-1)an-12+1(n≥2 n∈N*).③在③中，令n=2，结合a1=1，可解得：a2=1或2.又∵当n≥2时，an＞a1，∴舍去a2=1，得a2=2.同上，在③中，依次令n=3 n=4，可解得：a3=3 a4=4.猜想：an=n(n∈N*).下用数学归纳法证明：(ⅰ)n=1 2 3时，由已知条件及上述求解过程知显然成立.(ⅱ)假设n=k时命题成立，即ak=k(k∈N 且k≥3)，则由③式可得：(k-2)ak+12+3ak+1=kak2+1，把ak=k代入上式并解方程得：ak+1=或k+1 由于k≥3 ∴＜0，∴ak+1=.不符合题意，应舍去，故只有ak+1=k+1.所以，n=k+1时命题也成立.综上可知：数列{an}的通项公式为an=n(n∈N*).